Виталий Сигорский - Математический аппарат инженера

9. Обратная матрица. В обычной алгебре два числа, произведение которых равно единице, называют взаимно обратными . Число, обратное числу a обозначают через a -1и по определению aa -1= 1

- 37 -

Аналогично в матричной алгебре две квадратные матрицы, произведение которых равно единичной матрице, т.е. AA -1= A -1A = 1, называют взаимно обратными ( A -1обратна A). Однако дальше этого аналогия не проходит.

Выражение a -1b, где a и b — числа, можно представить как частное от деления b на a, но для матриц такое представление не имеет смысла и в общем случае A -1B ≠ BA -1. Поэтому вместо операции деления В на А различают левое частное A -1B и правое частное BA -1, которые сводятся к умножению слева или справа на обратную матрицу A -1.

Способ обращения матрицы проще всего установить, рассматривая решение системы n линейных уравнений с n неизвестными:

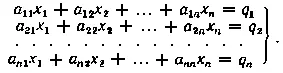
В матричной форме эта система уравнений запишется как Ax = q, где А — квадратная матрица n-го порядка, называемая матрицей системы : x и q — столбцевые матрицы неизвестных переменных и свободных членов:

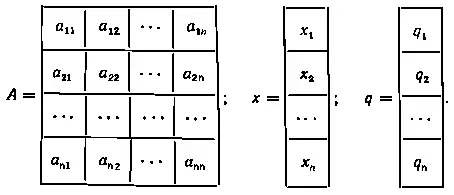
Матричное уравнение Ax = q решается умножением обеих его частей слева на обратную матрицу A -1т.е. A -1Ax = A -1q в результате получаем x = A -1q.

В соответствии с правилом Крамера неизвестные x k(k = 1, 2, ..., n) определяются соотношением:

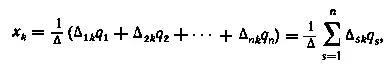
где Δ — определитель системы уравнений Δ sk— алгебраические дополнения.

- 38 -

Определитель Δ представляет собой числовую функцию, которая вычисляется по определенным правилам на основании квадратной таблицы, состоящей из коэффициентов системы уравнений

Табличное представление определителя Δ по форме совпадает с матрицей системы уравнений, т.е. состоит из тех же элементов и в том же порядке, что и матрица А. В таких случаях его называют определителем матрицы А и записывают Δ = detA.

Алгебраическое дополнение Δ skвычисляется как определитель матрицы, полученной удалением из матицы A s-й строки и k-го столбца, причем этот определитель умножается еще на (-1) s+k. Величину Δ skназывают также алгебраическим дополнением элемента a skматрицы A. Часто определитель матрицы А обозначается через |A|, а алгебраическое дополнение — через A sk.

Записав для всех элементов столбцевой матрицы x выражения по правилам Крамера, получим решение системы уравнений в виде:

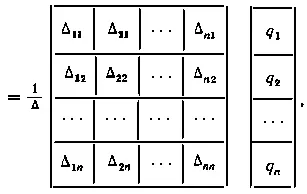
- 39 -

откуда, сравнивая с A -1q, имеем

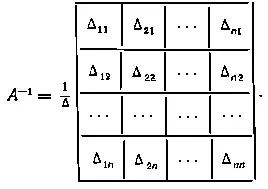
Из полученного выражения следует правило определения обратной матрицы: 1) элементы a ijданной матрицы A n-го порядка заменяются их алгебраическими дополнениями Δ ij: 2) матрица алгебраических дополнений транспонируется, в результате чего получаем присоединенную или взаимную матрицу к А ( она обозначается через AdjA); 3) вычисляется определитель Δ матрицы А и присоединенная матрица AdjA умножается на величину, обратную этому определителю.

Обратная матрица существует для матрицы А при условии, что detA ≠ 0. Такие матрицы называются неособенными , в отличие от особенных (вырожденных), определитель которых равен нулю. Ниже вычисление обратной матрицы иллюстрируется примером:

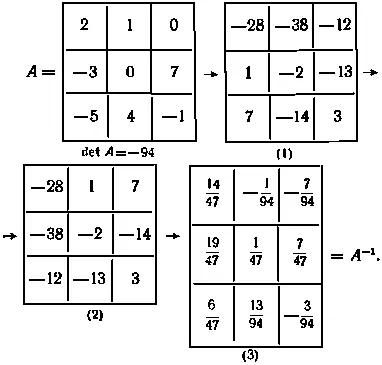
- 40 -

Матрица, обратная произведению двух матриц, равна переставленному произведению матриц, обратных исходным, т.е. (AB) -1= B -1A -1. Действительно, умножив обе части этого равенства на АВ, приходим тождеству E = B -1A -1(AB), так как B -1(A -1A)B = B -1EB = B -1B =E, где E — единичная матрица n-го порядка.

10. Блочные матрицы. Часто матрицу удобно разбить вертикальными и горизонтальными линиями на блоки которые являются матрицами меньших размеров и при выполнении операций рассматриваются как элементы исходных матриц. Операции над блочными матрицами выполняются по сформулированным выше правилам при условии, что эти операции допускаются размерами соответствующих матриц.

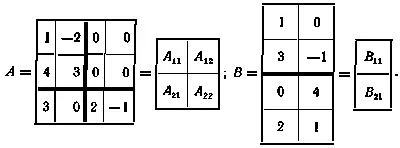
Пусть, например, матрицы А и В разбиты на блоки (жирными линиями) так, чтобы для соответствующих блоков имела смысл операция умножения, т.е.

По правилу умножения прямоугольных матриц можно записать:

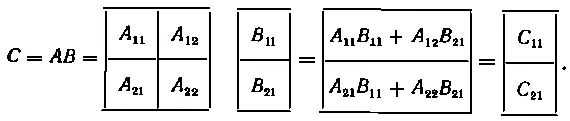
Вычислим блоки C 11и C 21матрицы C:

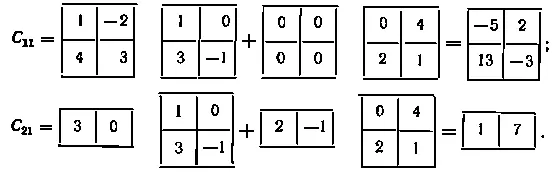
- 41 -

В результате имеем

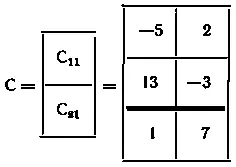
Конечно, тот же результат получается и при непосредственном перемножении матриц. Но разбиение на блоки позволяет оперировать с матрицами меньших размеров ( это бывает необходимо, например, когда не хватает места на бумаге или ячеек оперативной памяти машины) и особенно удобно, если можно выделить нулевые блоки.

1. Любая матрица является прямоугольной таблицей. Справедливо ли обратное утверждение, т.е. можно ли считать всякую прямоугольную таблицу матрицей? Если нет,то какие дополнительные требования выдвигаются с позиций матричной алгебры?

2. Какие из приведенных ниже совокупностей объектов представляют собой матрицы:

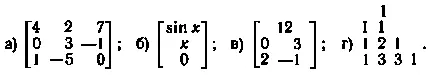
3. Укажите, какие из приведенных ниже матриц являются равными между собой (при x=2)%

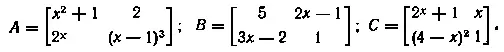
4. При каком значении x матрицы А и В равны:

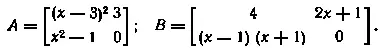
5. Найти сумму А + В и разность А — В матриц: