Иэн Стюарт - Математические головоломки профессора Стюарта

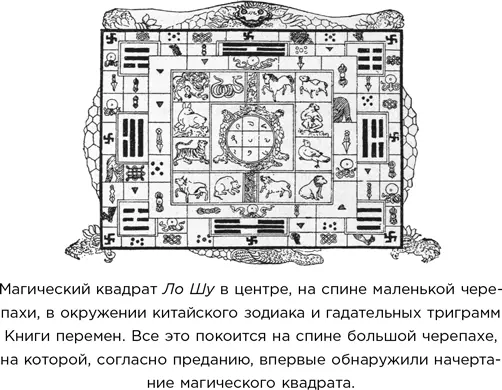
Сможете ли вы найти эти два принципиально разных решения? Ответ см. «Загадки разгаданные».

В 1782 г. Эйлер опубликовал задачу о 36 офицерах: можно ли построить офицеров шести полков, в каждом из которых по шесть офицеров разных рангов, в каре (то есть квадратом) 6 × 6 таким образом, чтобы в каждой шеренге и в каждой колонне присутствовали офицеры всех рангов из всех полков? Подобные расстановки получили название греко-латинских квадратов, потому что латинские (A, B, C, …) и греческие (α, β, γ, …) буквы можно использовать для обозначения рангов и полковой принадлежности. Эйлер нашел методы построения греко-латинских квадратов, порядок которых (то есть размер квадрата) является нечетным числом или имеет двойную четность, то есть кратен четырем.

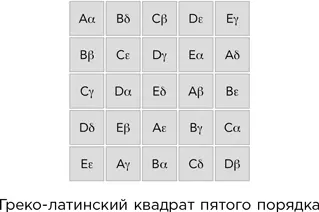
Эйлер предположил, что для порядка, выражаемого удвоенным нечетным числом, таких квадратов не существует. Для порядка 2 это очевидно, а в 1901 г. Гастон Тарри доказал это для порядка 6. Однако в 1959 г. Радж Чандра Бозе и Шарадчандра Шанкар Шриханде сумели при помощи компьютера отыскать греко-латинский квадрат порядка 22, а Эрнест Паркер нашел такой квадрат порядка 10. После этого все трое доказали, что гипотеза Эйлера неверна для всех удвоенных нечетных чисел, больших или равных 10.

Квадратные таблицы размером n × n, такие, что каждая строка и каждый столбец содержит все числа от 1 до n (каждое, понятно, по одному разу), получили известность как латинские квадраты, а греко-латинские квадраты были переименованы в ортогональные латинские квадраты. Эти темы входят в область математики, которую называют комбинаторикой, и применяются в области коммуникаций, в экспериментальном дизайне и при составлении расписаний всевозможных соревнований.

Полный шаблон судоку – это латинский квадрат, но в головоломке присутствуют и дополнительные условия по отношению к внутренним блокам 3 × 3. В 1892 г. французская газета Le Siècle напечатала на своих страницах головоломку, в которой из магического квадрата были удалены некоторые числа, и читатели должны были их восстановить. La France вплотную подошла к изобретению судоку, так как в ее магических квадратах использовались только цифры от 1 до 9. В решениях, кстати говоря, каждый из блоков 3 × 3 тоже содержал все девять цифр, но явно об этом нигде не говорилось.

Судоку в его современной форме предложил, вероятно, Говард Гарнс, а опубликована первая головоломка была анонимно в Dell Magazines в 1979 г. под названием «числовая площадь». В 1986 г. японская компания Nikoli публиковала такие головоломки в Японии под не слишком удобоваримым и заметным названием suji wa dokushin ni kagiru («все цифры по одному разу»). Позже название сократили до su doku . Газета The Times начала публиковать головоломки судоку в Великобритании в 2004 г., после того как Уэйн Гулд, написавший компьютерную программу, способную отыскивать решения практически мгновенно, обратился в редакцию с предложением о сотрудничестве. В 2005 г. судоку во всем мире стали модным увлечением.

Этим страшным словом обозначается боязнь числа 666.

В 1989 г. президент США Рональд Рейган и его жена Нэнси при переезде поменяли прежний адрес своего нового дома, 666 по Сен-Клу-роуд, на 668 по той же улице. Однако вряд ли этот случай можно приводить в качестве примера гексакосиойгексеконтагексафобии, поскольку вполне возможно, что Рейганы не боялись этого числа как такового, а просто хотели подстраховаться и избежать в будущем очевидных обвинений и возможных неловкостей.

С другой стороны… Когда Дональд Риган, шеф президентской администрации при Рейгане, опубликовал в 1988 г. свои мемуары «Под запись. От Уолл-стрит до Вашингтона», он написал, что Нэнси Рейган регулярно советовалась с астрологами, сначала с Джейн Диксон, а позже с Джоан Куигли. «Практически любое серьезное действие или решение Рейганов во время моего пребывания на посту главы администрации Белого дома заранее согласовывалось с какой-то женщиной в Сан-Франциско, которая рисовала гороскопы, чтобы убедиться в благоприятном расположении планет».

Число 666 обладает оккультным смыслом, потому что именно оно объявлено числом зверя в Откровении Иоанна Богослова (13:17–18): «И что никому нельзя будет ни покупать, ни продавать, кроме того, кто имеет это начертание, или имя зверя, или число имени его. Здесь мудрость. Кто имеет ум, тот сочти число зверя, ибо это число человеческое; число его шестьсот шестьдесят шесть».

Считается, что это число отсылает нас к нумерологической системе, которая на иврите называется «гематрия», а по-гречески – «изопсефия» и в которой числа обозначаются буквами алфавита. При этом возможно несколько вариантов обозначения: буквы алфавита можно пронумеровать последовательно, а можно сначала обозначить цифры 1–9, затем десятки 10–90, затем сотни 100–900 и т. д., сколько нужно (именно так записывали числа древние греки). Тогда сумма чисел, обозначаемых буквами имени человека, и будет численным значением этого имени.

За прошедшие века предпринимались бесчисленные попытки вычислить, кто такой зверь, упоминаемый в Откровении. Среди предположений фигурируют и Антихрист (написанный в подобных обвинениях на латыни как Antichristum ), и Римско-католическая церковь (обозначенная одним из вариантов титулования римского папы: Vicarius Filii Dei ), и Эллен Гулд Уайт (Ellen Gould White), одна из организаторов Церкви адвентистов седьмого дня. С чего бы вдруг? Ну, если считать только латинские числительные в ее имени, то получится:

что в сумме дает 666. Если вы считаете, что зверем был Адольф Гитлер, вы можете «доказать» это, начав нумерацию с A = 100:

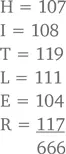
В сущности, процесс «доказывания» сводится к следующему: выбираете ненавистную фигуру на основании собственных политических или религиозных взглядов, а затем подгоняете нумерацию и, если необходимо, имя, чтобы получить нужный результат.

Однако не исключено, что все эти глубокомысленные рассуждения и далеко идущие выводы основаны на простом недопонимании – не говоря уже о сомнительности веры в то, что подобные вещи в принципе могут что-то значить; сегодня уже очевидно, что число 666, возможно, возникло в результате ошибки. Около 200 г. н. э. священник Ириней знал, что в нескольких ранних рукописях называется другое число, но приписывал это ошибкам писцов и утверждал, что именно 666 можно найти «во всех самых достоверных и древних списках». Но в 2005 г. ученые Оксфордского университета применили компьютерные технологии обработки изображений и попытались прочесть с их помощью нечитаемые прежде части самого раннего известного списка «Откровения» – экспоната № 115 из числа папирусов, обнаруженных при раскопках древнего Оксиринха. Этот документ, датируемый примерно 300 г. н. э., считается самой достоверной и определяющей версией канонического текста. Числом зверя в нем названо 616.