Иэн Стюарт - Математические головоломки профессора Стюарта

– Простите, Сомс, я просто надеялся получить кое-какие сравнительные данные о методах исследования из произведений коллеги… э-э… шарлатана из дома напротив.

– Тьфу! Этот человек – мошенник! Жулик, называющий себя детективом!

Откровенно говоря, временами Сомс бывает невыносим. Если подумать, он почти всегда такой.

– Бывали случаи, когда мне удавалось случайно выудить что-нибудь полезное из скучных творений моего нещадно эксплуатируемого коллеги, Сомс, – возразил я.

– Что, например? – агрессивно вопросил он.

– На меня сильное впечатление произвел такой его аргумент: «Если вы исключите невозможное, то, что останется, каким бы невероятным ни казалось, и будет…

– Ошибкой, – бесцеремонно закончил за меня Сомс. – Если то, что остается, по-настоящему невероятно, значит, вы почти наверняка приняли «по умолчанию» какое-то условие, когда объявляли все другие объяснения невозможными.

Последовательность никогда не значилась в числе добродетелей Сомса.

– Ну, может быть, но…

– Без всяких «но», Ватсап!

– Но ведь в других ситуациях вы соглашались…

– Тьфу! Реальность не бывает невероятной, Ватсап! Она может казаться таковой, но на самом деле ее вероятность составляет 100 %, потому что она уже случилась .

– Ну да, формально это так, но…

– Вот пример. Сегодня утром, когда вы, Ватсап, выходили купить эту лживую газетенку, я принял весьма неожиданного посетителя. Небезызвестного герцога Бамблфортского.

– Главный лондонский щеголь, – сказал я. – Благородный человек безукоризненной честности, образец для всех нас.

– Ну да, ну да. Тем не менее он проинформировал меня… Ну, он рассказал, что в Бамблфорт-холле был обед, на котором эрл Мондеринг, желая развлечь гостей, поставил в ряд десять винных стаканов и наполнил первые пять из них – вот так, – и Сомс продемонстрировал мне этот процесс наглядно, на наших собственных стаканах, наполнив их довольно кислой мадерой, от которой мы как раз решили избавиться. – Затем он предложил гостям переставить стаканы таким образом, чтобы полные чередовались с пустыми.

– Но это очень просто… – начал я.

– Если переставить четыре стакана, то да. Достаточно поменять второй с седьмым и четвертый с девятым. Вот так – (см. рисунок). – Однако эрл просил получить тот же результат, переставив всего два стакана.

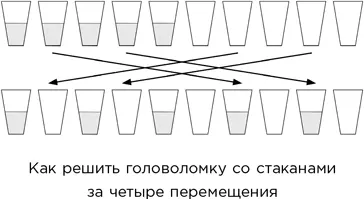
Я сложил пальцы перед собой в жесте глубокого размышления и через мгновение нарисовал грубый набросок первоначального и конечного расположения стаканов.

– Но, Сомс! Четыре названных вами стакана должны оказаться в разных местах! Так что без четырех перестановок не обойтись!

Он кивнул.

– Итак, Ватсап, вы только что исключили невозможное.

– Ну да, ей-богу, так я и сделал, Сомс! Неопровержимо.

Он начал набивать табак в свою трубку.

– И к какому же выводу вы придете, если я скажу, что, по словам герцога Бамблфортского, после того как все гости высказались примерно в таком же духе, эрл Мондеринг продемонстрировал верное решение.

– Я… ну…

– Вы вынуждены признать, что благородный герцог, наследник Британской империи и образец высокого благородства… на самом деле низкий лжец. Поскольку никакого решения не существует, как вы только что доказали.

Мое лицо вытянулось.

– Да, правда, все выглядит именно так… Нет, подождите, возможно, это вы не говорите мне…

– Мой дорогой доктор, я, честно признаюсь, иногда действительно умалчиваю кое-что, исключительно в ваших интересах, но не в данном случае. Даю слово.

– Но тогда… Я шокирован поведением герцога.

– Оставьте, Ватсап. Имейте веру в британский характер.

– Эрл обманывал?

– Нет-нет-нет. Ничего подобного. Вы способны на большее. В этой ситуации может быть и другое вполне прозаическое объяснение, которое вы проглядели. Более того, могу с уверенностью предсказать, что через несколько минут вы сами будете говорить мне, что решение очень простое и что догадаться может даже ребенок.

После этого Сомс рассказал мне, что сделал Мондеринг.

– Ну, здесь даже ребенок дога… – начал я, но вдруг резко остановился. Должен со всей откровенностью признать, что в этот момент я покраснел как рак.

Какое решение предложил Мондеринг? Ответ см. в главе «Загадки разгаданные».

Идиллическая сцена на морском берегу: тихая бухта, волны разбиваются о скалы, покрытые водорослями и увешанные гроздьями моллюсков. Кажется, всюду царит сонное спокойствие. На самом деле эти неподвижные скопления мидий – царство непрекращающейся активности; чтобы ее увидеть, нам просто придется ускорить течение времени. При покадровой съемке видно, что моллюски в группах постоянно находятся в движении. Они прикрепляются к камням при помощи особых нитей, которые выделяет нога. Открепляя одни нити и добавляя другие в новых местах, мидия может управлять своим положением на камнях. С одной стороны, мидии любят находиться рядом с себе подобными, потому что вероятность того, что их оторвет от камня волнами, в этом случае заметно меньше. С другой стороны, если рядом нет других мидий, которые составили бы конкуренцию, можно добыть больше пищи. Оказываясь перед такой дилеммой, мидии делают то, что сделало бы на их месте большинство здравомыслящих организмов: идут на компромисс. Они размещаются таким образом, что у каждой мидии оказывается много близких соседей, но мало дальних. То есть они собираются группами. Эти группы – заплатки на дне – видны невооруженным глазом, но вот как они формируются, заметить невозможно.

В 2011 г. Моник де Джагер и ее коллеги применили математику случайного блуждания к моделированию того, как могла сформироваться у мидий групповая стратегия. Случайное блуждание часто сравнивают с движением пьяного по дорожке: то вперед, то назад, без всякой очевидной системы. Если добавить еще одно измерение, получится, что случайное блуждание на плоскости – это серия шагов, длины и направления которых выбираются случайным образом. Разные правила выбора – разные распределения вероятностей для длин и направлений – дают случайные блуждания с разными свойствами. В броуновском движении длины шагов распределяются по колоколовидной кривой вблизи одного конкретного среднего значения шага. В блужданиях Леви [19] Случайные блуждания Леви – марковский случайный процесс с дискретным временем, плотность распределения индивидуальных приращений в котором имеет протяженный степенной «хвост». У такого распределения отсутствует дисперсия, поэтому к данному процессу не применима центральная предельная теорема, и положение точки, совершающей случайные блуждания Леви, даже после большого числа шагов, не описывается нормальным, или гауссовым, распределением. – Прим. ред. вероятность того или иного шага пропорциональна некоторой фиксированной степени его длины, в результате чего многочисленные короткие шаги время от времени прерываются гораздо более длинным шагом.