Иэн Стюарт - Математические головоломки профессора Стюарта

– Да, Сомс, я понимаю. Это слегка замаскированная версия метода Пеано, который мы ранее отвергли именно из-за его тривиальности.

– Так что, Ватсап, если разрешить экспоненциальные выражения и логарифмы, игра сразу же закончится.

Я согласился – не без грусти, поскольку он сразу же взял свой кларнет и вновь завел бесконечную пьесу какого-то малоизвестного восточноевропейского композитора, в которой не было ни ритма, ни мелодии. Звук походил на вопль кота, попавшего между валками для отжимания белья. Кота, которому медведь наступил на ухо. Притом охрипшего.

Черное настроение поглотило Сомса окончательно и бесповоротно.

На этом заканчивается «Знак одного».

Правда, я так и не рассказал вам, что такое субфакториал. Ну, ничего, в следующий раз.

Пора объяснить, что такое субфакториалы.

Предположим, что у каждой из n дам имеется шляпка. Все они складывают свои шляпки в одно место, затем каждая из них берет какую-нибудь случайную шляпку и надевает на себя. Сколькими способами можно это сделать, чтобы ни на одной из дам не оказалось ее собственной шляпки? Такое размещение называется беспорядком .

К примеру, если дам три – скажем, Александра, Бетани и Валерия, – то шляпки между ними можно распределить шестью способами:

АБВ АВБ БАВ БВА ВАБ ВБА.

Для АБВ и АВБ Александра получает свою собственную шляпку, так что беспорядка не возникает. Для БАВ собственную шляпку получает Валерия, а для ВБА – Бетани. Это оставляет нам два варианта беспорядка: БАВ и ВАБ.

Если дам четыре – предположим, к группе присоединилась еще Грейс – существует 24 варианта расстановки:

однако в 15 из них (вычеркнутые) кто-нибудь из дам получает свою собственную шляпку. (Убираем все с А в первой позиции, с Б во второй, с В в третьей и с Г в четвертой.) В результате получаем 9 вариантов беспорядка.

Число вариантов беспорядка из n объектов и есть субфакториал (обозначается! n или n ¡). У этого понятия множество определений. Простейшее из них, вероятно,

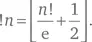
Первые значения этой величины

Бросание монетки – фундамент теории вероятностей, поскольку орел или решка выпадают на ней с равной вероятностью. Бросание монетки считается живым воплощением случайности. С другой стороны, моделью монетки может служить простая механическая система, и ее поведение полностью определяется начальными условиями броска – в первую очередь вертикальной скоростью, начальной скоростью вращения и ориентацией оси вращения. Это, собственно говоря, делает движение монетки неслучайным. Так откуда же берется случайность в бросание монетки? Я вернусь к этому вопросу после описания открытия, имеющего ко всему этому непосредственное отношение.

Перси Диаконис, Сьюзен Холмс и Ричард Монтгомери показали, что на самом деле бросание монетки – не совсем «честная» жеребьевка. Существует небольшой, но заметный сдвиг вероятности: при бросании монетка с несколько большей вероятностью падает на ту же сторону, на которой она лежала на большом пальце. В реальности вероятность ее падения именно в таком положении составляет приблизительно 51 %. В своем исследовании ученые предполагали, что монетка при падении не подскакивает, что разумно при падении на землю, особенно в траву, или для того случая, когда ее ловят на лету, но не тогда, когда она падает на деревянный стол.

Вероятность 51 % становится статистически значимой только после примерно 250 000 бросков. Возникает этот сдвиг потому, что ось, вокруг которой вращается монетка, может и не быть горизонтальной. В предельном случае представьте, что ось располагается под прямым углом к монетке, так что монетка, вращаясь, всегда остается горизонтальной, как гончарный круг. В таком случае она всегда будет приземляться той же стороной, которой лежала, то есть вероятность ее непереворачивания составит 100 %. Другой предельный случай – ось горизонтальна, и монетка кувыркается в воздухе. Хотя в принципе конечное состояние монетки в этом случае определяется начальной вертикальной скоростью и скоростью вращения в воздухе, даже небольшие ошибки в этих параметрах приводят к тому, что монетка падает той же стороной кверху лишь в 50 % случаев. При таких бросках небольшие ошибки приводят к случайному взаимодействию механической системы и монетки.

Как правило, ось вращения монетки не находится ни в одном из крайних положений, а расположена в каком-то промежуточном, близком к горизонтали. Поэтому возникает легкий сдвиг вероятности в сторону падения той же стороной вверх. Подробные расчеты дали 51 % вероятности. Эксперименты с монеткобросательным автоматом подтвердили этот результат с разумной достоверностью.

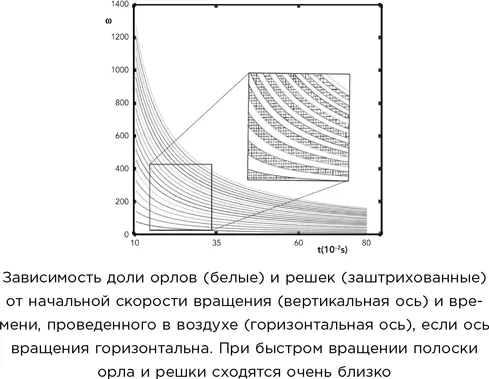
На практике бросание настоящей монетки все-таки дает случайный результат с 50 % вероятностью, причем вовсе не по приведенным причинам. Дело в том, что начальная ориентация монетки на пальце тоже случайна. Если говорить о длинных сериях, то монетка в половине случаев взлетает орлом кверху, а в половине – решкой кверху. Это снимает сдвиг на 1 %, потому что при броске неизвестно, из какого именно положения стартует монетка.

Дополнительную информацию см. в главе «Загадки разгаданные».

Предположим, что Алиса и Боб – традиционные участники криптографической переписки – хотят сыграть в покер, точнее, в пятикарточный стад. Но Алиса живет в Австралии, в Алис-Спрингс, а Боб – в Англии, в Боббингтоне. Но возможно, они могли бы пересылать друг другу карты по почте? Главная проблема – как раздать карты, то есть дать каждому игроку «в руки» по пять карт. Как могут при этом оба игрока быть уверены, что каждому из них достались карты из одной колоды и что второй игрок их не знает?

Если Боб просто отправит Алисе в конверте пять карт, она не сможет быть уверена, что он их не видел; более того, когда Боб выкладывает карты, которые будто бы находятся у него на руках, она не может быть уверена, действительно ли у него только пять карт, или в его распоряжении находится вся остальная колода и он только делает вид, что использует только законные пять карт, сданные ему в начале игры.