Иэн Стюарт - Математические головоломки профессора Стюарта

Иногда самые простые идеи приводят к загадочным результатам. Попробуйте умножить 123456789 на 1, 2, 3, 4, 5, 6, 7, 8 и 9. Что вы заметили? Когда закономерность перестает работать?

Ответы см. в главе «Загадки разгаданные». Расширение темы в главе «123456789 раз по X. Продолжение».

Горы бумаг, испещренных загадочными письменами, росли как грибы на всех горизонтальных поверхностях обиталища Сомса. В этом, как вы понимаете, ничего необычного не было; миссис Сопсудс часто и притом совершенно безрезультатно ругала его за способ хранения бумаг, больше напоминающий глубокие залежи мусора. Но на этот раз каракули на листах представляли собой результаты суммирования.

– Я могу получить 8 из двух единиц, не прибегая к помощи гипотетического выражения для 7, – объявил я. – Вот так:

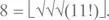
Но даже под угрозой смерти я не в состоянии получить 7.

– Действительно, это число, судя по всему, является камнем преткновения, – согласился со мной Сомс. – Но ваш результат позволяет нам продвинуться и другими способами:

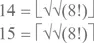
где, разумеется, вместо восьмерки мы при необходимости подставляем ваше выражение. Я мог бы расписать это выражение полностью…

– Нет-нет, Сомс, вы меня убедили!

– Но теперь у нас образовалось еще две лакуны на 12 и 13. Однако, Ватсап, я подозреваю, что эти проблемы взаимосвязаны. Так, посмотрим… Ну да,

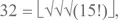
а 15 на основе двух единиц у нас уже есть. Тогда

и далее

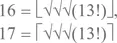
и, наконец,

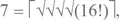
что вполне удовлетворительно решает нашу проблему. Таким образом, подставляя по очереди выражения для всех использованных чисел, получаем, что

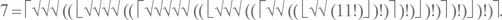
– Мне невыносимо стыдно, что я не увидел этого сразу.

– Неужели это простейшее решение, Сомс? – вопросил я, проглотив комок в горле. – Надеюсь, что нет!

– Понятия не имею. Возможно, кто-то изобретательный смог бы придумать что-нибудь получше. В подобных вещах трудно сказать наверняка. Я уверен, что тот, кто сумеет превзойти наши слабые усилия, немедленно известит нас телеграммой.

– Во всяком случае, – сказал я, – если нам удастся выразить какое-то целое число при помощи двух единиц, то теперь мы сможем выразить при помощи четырех единиц все числа в диапазоне от n – 17 до n + 17.

– Вот именно, Ватсап. Наша задача упрощается с каждой минутой. Все, что нам нужно, – это последовательность чисел, каждое из которых превосходит предыдущее не более чем на 35, так, чтобы эти интервалы с двух сторон перекрывали пробел. Это позволит нам добраться до наибольшего из таких чисел плюс 17.

– Что означает… – начал я…

– Что мы должны действовать систематически!

– Именно.

– Мы уже добрались… напомните мне, Ватсап. Загляните в свои обширные записи.

Я с головой зарылся в несколько высоких бумажных башен и в конце концов отыскал свой блокнот под чучелом какого-то скунса.

– Мы дошли до 32, Сомс, если учесть замечание, которое вы мимоходом сделали во время поиска выражения для 7.

– И разумеется,

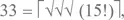
– сказал он. – Очень хорошо. Таким образом, в идеале нам нужно выразить числа 68, 103, 138 и т. д. через две единицы. Но мы можем пользоваться при этом готовыми выражениями для маленьких чисел, если так будет удобнее. Лишь бы разница между двумя соседними числами не была больше 35.

Несколько часов усиленных расчетов – и новые кипы бумаги – дали нам короткий, но важный список:

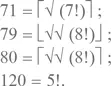
Но на этом все и застопорилось.

– Возможно, я слишком поспешно отказался от использования двойных факториалов, Ватсап.

– Очень может быть, Сомс.

Сомс кивнул и записал:

105 = 7!!

Затем, в порыве внезапного озарения, добавил:

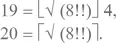
И воскликнул:

– Если нам удастся найти способ записать 18 при помощи двух единиц, то доступный нам диапазон вокруг целого числа, выражаемого через две единицы, увеличится: мы тогда сможем гарантировать число от n – 20 до n + 20, – он прервался, чтобы перевести дух, и добавил: – Если же нет, то пропущенными в этом диапазоне окажутся только числа n – 18 и n + 18, которые нам, может быть, удастся выразить как-то иначе.

– Мне кажется, пора подвести промежуточный итог, – сказал я и еще раз внимательно просмотрел наши накопившиеся каракули. – По-моему, мы уже выразили через четыре единицы все числа от 1 до 33. Далее

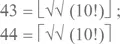
требуют только двух единиц, так что мы немедленно заполняем все пропуски между 26 и 61. Возникает пробел на 62 (потому что это 44 + 18, а на выражении 18 через две единицы мы застряли), но 63 и 64 у нас есть. Далее, опираясь на 80, мы можем добраться до 97. На 98 опять возникает пробел, но 99 и 100 можно получить.

– И намного проще, кстати говоря, – заметил Сомс:

99 = 11/0,1 × 0,1;

100 = 1/(0,1 × 0,1);

101 = 1/(0,1 × 0,1) + 1.

– Таким образом, у нас есть все вплоть до 100, – сказал я, – за исключением 62 и 98.

– Но о 98 позаботится 105, вместе со всеми остальными числами вплоть до 122, – сказал Сомс.

– О, я и забыл, что у нас есть 105 из двух единиц.

– А поскольку 120 = 5! то есть тоже выражается через две единицы, мы можем добраться до 137. Более того, у нас есть еще 139 и 140.

– Так что единственные пробелы до 140 – это 62 и 138, – сказал я.

– Похоже на то, – сказал Сомс. – Интересно, можно ли заполнить эти пробелы каким-то другим способом?

Сможете ли вы найти способ записать 62 и 138 при помощи четырех единиц, не используя ничего более эзотерического, чем те функции, которые Сомс и Ватсап уже использовали? Ответ см. в главе «Загадки разгаданные».

Сомс и Ватсап все еще не закончили. Но финал уже близок: «Знак одного» завершается в главе «Знак одного. Часть четвертая – завершение».