Иэн Стюарт - Математические головоломки профессора Стюарта

– Согласен! И совершенно очевидно, – заявил тут же Сомс, – что такое выражение для 7 сразу же даст нам выражение для 8.

– Э-э… правда?

– Естественно. Поскольку 7! = 5040, квадратный корень из этого числа равен 70,99, а следующий квадратный корень равен 8,42, мы делаем вывод, что

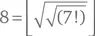
– Так что не впервые в истории человечества ключом к загадке является число 7! (В этих словах, дорогой читатель, он подчеркивал число 7 восклицательным знаком, а не имел в виду факториал. Пожалуйста, обратите на это внимание, я об этом уже упоминал.)

Сомс нахмурился.

– Я могу сделать это, если использую двойной факториал.

– Вы имеете в виду факториал факториала?

– Нет.

– Субфакториал? Вы пока не объяснили…

– Нет. Двойной факториал – это немного запутанная штука; он равен

n !! = n × ( n – 2) × ( n – 4) × … × 4 × 2

для четных n и n !! = n × ( n – 2) × ( n – 4) × … × 3 × 1

для нечетных. Так, к примеру,

6!! = 6 × 4 × 2 = 48.

Корень квадратный из этого числа равен 6,82, а его потолок равен 7.

Я послушно записал:

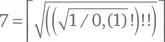
Но Сомс по-прежнему выглядел недовольным.

– Проблема в том, Ватсап, что при помощи введения все более загадочных и вычурных арифметических функций можно с легкостью выразить вообще любое число. К примеру, мы могли бы воспользоваться арифметикой Пеано.

Я шумно запротестовал:

– Сомс, вы же знаете, что наша хозяйка не устает жаловаться на ваш кларнет. Она никогда не позволит поставить к нам пианино!

– Я говорил о Джузеппе Пеано, так звали итальянского математика и специалиста по логике, Ватсап.

– Откровенно говоря, не такая уж большая разница. Я не уверен, что миссис Сопсудс…

– Тихо! Согласно арифметической аксиоматике Пеано, наследником любого целого числа является число

s ( n ) = n + 1.

– Так что Пеано вполне мог бы записать:

1 = 1,

2 = s (1),

3 = s ( s (1)),

4 = s ( s ( s (1))),

5 = s ( s ( s ( s (1)))),

и эта последовательность будет продолжаться до бесконечности. В этой системе любое целое число можно выразить при помощи всего одной единицы. Или даже одного нуля, поскольку 1 = s (0). Это слишком тривиально, Ватсап.

Сможете ли вы найти способ записать 7 с использованием только двух единиц, не прибегая ни к чему более экзотическому, чем функции, которые Сомс и Ватсап использовали прежде, чем начали спорить о двойных факториалах и наследниках? Ответ см. «Загадки разгаданные».

Сомс и Ватсап еще не закончили. «Знак одного» продолжается в главе «Знак одного. Часть третья».

Р. Х. Бинг – американский математик, родился в Техасе, специализировался на геометрической топологии. Что означает Р. Х.? Ну, как сказать… Его отца звали Руперт Генри, но его мать считала, что для Техаса такое имя звучит слишком по-британски, поэтому при крещении ребенка она укоротила его до предела, оставив одни инициалы. Поэтому Р. Х. означает Р. Х., и ничего больше. Это вызывало, конечно, некоторое удивление, но не доставляло ему серьезных неудобств – до тех пор, пока Бинг не обратился за визой для поездки куда-то. Когда его попросили назвать имя, он, предвидя обычную реакцию, сказал: «R-only H-only Bing» [18] «Просто Р. просто Х. Бинг». – Прим. пер. .

В результате он получил визу, выданную на имя Ронли Хонли Бинга.

Это математическая загадка, которая была решена более двух тысяч лет назад и долгое время преподавалась в школах, но теперь уже не преподается – по разумным, вероятно, соображениям. Однако с ней стоит познакомиться, поскольку она намного эффективнее того метода, который используется вместо нее. Кроме того, она позволяет установить связь со многими важными математическими понятиями более высоких уровней.

Люди, как правило, любят выводить каракули. Нередко можно увидеть, как кто-то, разговаривая по телефону, бездумно заштриховывает шариковой ручкой, к примеру, все буквы «о» на газетной странице. Или выводит извилистые линии, которые длятся и длятся без конца, свиваясь в какие-то неправильные спирали. Слово doodle, обозначавшее первоначально глупца, впервые ввел, судя по всему, сценарист Роберт Рискин в комедии 1936 г. «Мистер Дидс переезжает в город»; в фильме мистер Дидс говорит о каракулях (doodle) как о средстве, помогающем человеку думать.

Если математик рисует каракули (а большинство из них грешат этим), он вполне может нарисовать, к примеру, прямоугольник. Что можно сделать с прямоугольником? Можно заштриховать его, можно закрутить вдоль сторон спиралеобразные линии… а можно отрезать от него кусок с одной стороны и получить прямоугольник поменьше. После этого естественно – и, кстати говоря, типично для ментальности рисовальщика каракулей – повторить проделанную процедуру.

Что при этом происходит? Может быть, вам, прежде чем читать дальше, захочется самому нарисовать пару прямоугольников.

Ну, хорошо, продолжаем. Я начал с длинного узкого прямоугольника, и вот что получилось.

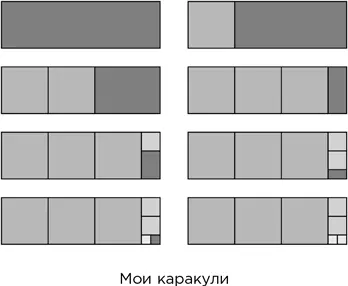
В конце концов я получил маленький квадратик, на котором мой прямоугольник закончился.

Всегда ли так получается? Всякий ли прямоугольник в конце концов заканчивается? Это хороший вопрос, способный дать математику пищу для размышлений.

Какого размера был мой прямоугольник? Ну, последний рисунок показывает, что:

• сумма сторон двух маленьких квадратиков равна стороне среднего квадрата;

• сумма сторон двух средних квадратов и одного маленького квадратика образует сторону большого квадрата и равна при этом одной из сторон прямоугольника;

• сумма сторон трех больших квадратов и одного среднего равна второй стороне прямоугольника.

Если сторона маленького квадратика равна единице, то сторона среднего квадрата равна 2, а сторона большого равна 2 × 2 + 1 = 5. Следовательно, короткая сторона прямоугольника равна 5, а длинная равна 3 × 5 + 2 = 17. Таким образом, я начал с прямоугольника размером 17 × 5.

Это интересно: глядя на то, как складываются квадраты, я могу определить размеры своего прямоугольника. Более тонкий момент: если процесс завершается, это означает, что обе стороны первоначального прямоугольника нацело делятся на одно и то же число – сторону последнего изъятого квадрата. Иными словами, отношение его сторон имеет форму p/q , где p и q – целые. Что делает его рациональным числом.