Иэн Стюарт - Математические головоломки профессора Стюарта

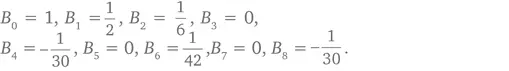
А вот другое, эквивалентное утверждение: число p является простым в том, и только том случае, если

[1 p − 1 + 2 p − 1 + 3 p − 1 + … + ( p − 1 ) p − 1 ] + 1

делится на p (Guiseppe Giuca, 1950).

Контрпример, если таковой существует, должен иметь по крайней мере 13 800 знаков (David Borwein, Jonathan Borwein, Peter Borwein and Roland Girgensohn, 1996).

Если p n – это n -е простое число, то

(Dorin Andrica, 1986).

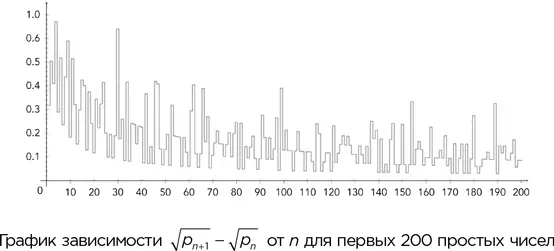
Имран Гори использовал данные о наибольших промежутках между простыми числами, чтобы подтвердить эту гипотезу для n вплоть до 1,3002 × 10 16. На рисунке вы можете видеть зависимость √( p n +1) – √ p n от n для первых 200 простых чисел. Число 1 располагается в самом верху вертикальной оси, а все остальные пики, показанные на графике, – ниже. Они явно уменьшаются с увеличением n , но мы не можем быть уверены, что на каком-то очень большом n не наблюдается гигантский пик, превосходящий 1. Чтобы данная гипотеза оказалась ошибочной, где-то должен существовать особенно большой промежуток между двумя очень большими последовательными простыми числами. Это представляется весьма маловероятным, но и полностью исключить такой вариант пока невозможно.

Любое целое число a , не равное −1 и не являющееся полным квадратом, есть первообразный корень по модулю бесконечного числа простых чисел. То есть всякое число от 1 до p − 1 есть некая степень a минус некое число, кратное p . Существуют конкретные формулы для количественного соотношения таких простых чисел по мере их увеличения (Emil Artin, 1927).

При n > 1 существует по крайней мере четыре простых числа между p ² и p ² n +1(Henri Brocard, 1904). Ожидается, что это верно; более того, по идее должны быть верны куда более сильные утверждения.

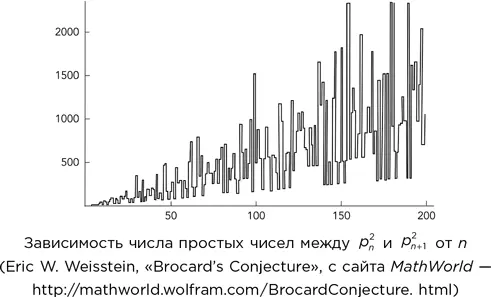
Промежуток p n +1− p n между последовательными простыми числами для больших n не превосходит (ln p n )² с постоянным коэффициентом (Harald Cramér, 1936).

Крамер доказал аналогичное утверждение, в котором вместо (ln p n )² фигурирует 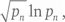при условии что верна гипотеза Римана – возможно, самая важная нерешенная проблема математики (см. «Кабинет…»).

Величина 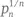строго уменьшается (Farideh Firoozbakht, 1982 г.). Это означает, что 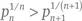для любого n . Это утверждение верно для всех целых чисел вплоть до 4 × 1018.

Пусть π2 ( x ) обозначает число простых чисел p ≤ x , таких, что p + 2 также простое число. Определим постоянную простых чисел-близнецов

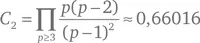
(где символ П указывает на произведение по всем простым числам p ≥ 3). Тогда гипотеза заключается в том, что

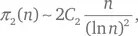
где знак ~ означает, что данное отношение стремится к 1 по мере того, как n становится сколь угодно большим (Godfrey Harold Hardy and John Edensor Littlewood, 1923).

Существует также вторая гипотеза Харди – Литтлвуда (см. ниже).

Начнем с простых чисел

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …

и вычислим разницу между соседними членами последовательности:

1, 2, 2, 4, 2, 4, 2, 4, 6, 2, …

Повторим те же вычисления для новой последовательности, не обращая внимания на знак, и продолжим в том же духе. Пять первых последовательностей будут выглядеть следующим образом:

1, 0, 2, 2, 2, 2, 2, 2, 4, …

1, 2, 0, 0, 0, 0, 0, 2, …

1, 2, 0, 0, 0, 0, 2, …

1, 2, 0, 0, 0, 2, …

1, 2, 0, 0, 2, …

Гилбрейт и Прот предположили, что первым членом каждой из этих последовательностей всегда будет 1, сколько бы раз мы ни повторяли процедуру (Norman Gilbreath, 1958, François Proth, 1978).

В 1993 г. Эндрю Одлизко проверил эту гипотезу для первых 3,4 × 1011 последовательностей.

Всякое четное целое число, большее 2, можно выразить как сумму двух простых чисел (Christian Goldbach, 1742).

Т. Оливейра-и-Силва проверил эту гипотезу на компьютере для n ≤ 1,609 × 10 18.

Каждому элементу множества последовательных составных чисел можно поставить в соответствие отдельное простое число, которое является его делителем (C. A. Grimm, 1969).

К примеру, если взять составные числа 32, 33, 34, 35, 36, то им можно поставить в соответствие простые числа 2, 11, 17, 5, 3.

В 1912 г. Эдмунд Ландау перечислил четыре фундаментальные проблемы, связанные с простыми числами и известные в настоящее время как проблемы Ландау. Первые три – это гипотеза Гольдбаха (см. выше), гипотеза о простых числах-близнецах (см. ниже) и гипотеза Лежандра (см. ниже). Четвертая проблема выглядит так: существует ли бесконечно много простых чисел p , таких что p − 1 является полным квадратом? То есть p = x ² + 1 для целого x .

Вот первые несколько таких чисел: 2, 5, 17, 37, 101, 197, 257, 401, 577, 677, 1297, 3137, 4357, 5477, 7057, 8101, 8837, 12 101, 13 457, 14 401 и 15 377. А вот пример побольше (но ни в коем случае не самый большой):

p = 1, 524, 157, 875, 323, 883, 675, 049, 535, 156, 256, 668, 194, 500, 533, 455, 762, 536, 198, 787, 501, 905, 199, 875, 019, 052, 101

x = 1, 234, 567, 890, 123, 456, 789, 012, 345, 678, 901, 234, 567, 890.

В 1997 г. Джон Фридлендер и Хенрик Иванец доказали, что существует бесконечно много простых чисел вида x 2+ y 4для целых x, y . Первые из этого ряда: 2, 5, 17, 37, 41, 97, 101, 137, 181, 197, 241, 257, 277, 281, 337, 401 и 457. Иванец доказал, что существует бесконечно много чисел вида x ² + 1, имеющих не более двух простых множителей.

Близко, но не то.

Адриан-Мари Лежандр предположил, что для любого положительного n существует простое число, лежащее между n ² и ( n + 1)². Это утверждение могло бы быть следствием из гипотезы Андрики (см. выше) и гипотезы Опперманна (см. ниже). Из гипотезы Крамера (см. выше) следует, что гипотеза Лежандра верна для всех достаточно больших чисел. Известно, что она верна вплоть до 1018.