Иэн Стюарт - Математические головоломки профессора Стюарта

– Интересно, как далеко можно продвинуться, если использовать четыре единицы .

Внутренне я ликовал, поскольку в нем явно пробудился интерес. А вслух сказал:

– Да, я понимаю. Теперь √1 = 1 и 1! = 1, так что «бесплатно» ничего не возникает. Это усложняет задачу, но делает ее, возможно, более достойной нашего внимания.

Он хмыкнул, и я поспешил реализовать свое крохотное преимущество. Лучший способ заинтересовать Сомса состоит в том, чтобы попробовать решить задачу самостоятельно и потерпеть неудачу.

– Понятно, что 1 = 1 × 1 × 1 × 1,

а также

2 = (1 + 1) × 1 × 1,

3 = (1 + 1 + 1) × 1,

4 = 1 + 1 + 1 + 1,

но выражение для 5 мне уже не дается.

Сомс поднял одну бровь.

– Вы могли бы рассмотреть выражение

5 = (1/0,1)/(1 + 1).

– Хм, хитро! – воскликнул я, но Сомс только фыркнул. – Но как насчет 6? – продолжал я. – Я вижу, как получить шестерку с использованием факториала:

6 = (1 + 1 + 1)! × 1.

На самом деле мне нужны только три единицы, но от всех лишних легко избавиться посредством умножения на них.

– Элементарно, – пробормотал он. – А рассматривали ли вы такой вариант, Ватсап?

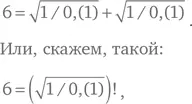
если вы настаиваете на использовании факториалов. Разумеется, чтобы использовать все четыре единицы, вы можете умножить на 1 × 1, или на 1/1, или прибавить 1–1.

Я непонимающе воззрился на формулу.

– Я узнаю десятичную точку, Сомс, но что означают скобки вокруг 1?

– Период, – ответил Сомс устало. – Нуль запятая 1 в периоде соответствует 0,11111… до бесконечности. Единица в периоде дает число, равное в точности 1/9. Разделив на это единицу, получим 9, корень из 9 равен 3…

– А дальше 3 + 3 = 6, – возбужденно вскричал я. – И еще, конечно,

7 = (1 + 1 + 1)! + 1

обходится без всяких корней. Но 8 – совсем другое дело…

– Обратите внимание, пожалуйста, – сказал Сомс.

8 = 1/0,(1) – 1 × 1

9 = 1/0,(1) + 1 – 1

– Ага! Вот это да! И дальше

10 = 1/0,(1) + 1 – 1

11 = 1/0,(1) + 1 + 1

и…

– Вы щедро тратите свои единицы, – заметил Сомс. – Лучше приберечь их для дальнейшего.

Он написал:

10 = 1/0,1

11 = 11

и добавил:

– Обратите внимание на отсутствие символа периода, Ватсап. На этот раз это обычная десятичная дробь 0,1. А-а, и вам следует домножить то и другое на 1 × 1, чтобы не оставлять лишних единиц или потратить их еще каким-то способом из тех, о которых я упоминал. Но вообще-то можно опускать эти лишние единицы, ведь позже мы найдем, куда их можно употребить.

– Да! Вы имеете в виду что-то вроде

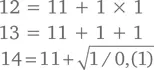
и т. д.?

По губам Сомса промелькнула тень улыбки.

– Вы точно все схватили, Ватсап!

– Но как насчет 15? – спросил я.

– Тривиально, – вздохнул он и написал:

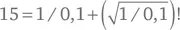
К этому я триумфально добавил:

и Сомс одобрительно кивнул.

– Вот теперь задача начинает становиться интересной, – заметил он. – Как насчет 23? Справитесь?

– Есть, Сомс! – воскликнул я.

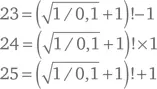
– Мы помним, – пояснил я, – что 4! = 24, как вы столь мудро заметили. Здорово, Сомс! Хотя 26 я не смог бы выразить, даже если бы на кону была моя жизнь.

– Ну… – начал он и остановился.

– Ага, застряли, не так ли?

– Ни в малейшей степени. Я просто думал о том, есть ли необходимость вводить новый символ. Конечно, он немало облегчит нам жизнь. Ватсап, слышали ли вы когда-нибудь о функциях округления, которые еще называют «пол» и «потолок»?

Мой взгляд против моей воли метнулся за подсказкой вниз, к ногам, а затем вверх, поверх головы Сомса, но вдохновение меня не осенило.

– Вижу, что не слышали, – сказал Сомс. «Откуда он знает, что я думаю? – подумал я. – Это даже…»

– Жутковато… да, разве не так? Я читаю вас, как открытую книгу, Ватсап. И эта книга, вероятно, «Сказки матушки Гусыни». Так вот эти функции выглядят так:

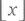= наибольшему целому числу, меньшему или равному x (пол, или округление вниз);

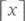= наименьшему целому числу, большему или равному x (потолок, или округление вверх), и вы скоро поймете, что они незаменимы в задачах вроде этой.

– Прекрасно, Сомс. Хотя я, признаюсь, не понимаю…

– Идея, Ватсап, в том, что посредством этих функций мы можем выразить полезные небольшие числа при помощи только двух единиц. К примеру,

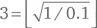– еще один способ выразить 3, использовав всего две единицы, а

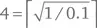– новый способ. – Видя мое недоумение, он добавил: – Обратите внимание,√1/ 0.1 = √10 = 3.162. Пол от этого числа равен 3, а потолок – 4.

– Ну да… – с сомнением проговорил я.

– Тогда мы идем дальше, потому что

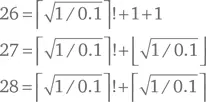
Не говоря уже о других возможных вариантах.

Тысячи разрозненных мыслей метались в моей голове. Одна в конце концов выступила перед.

– Но, Сомс, я только сейчас понял, что

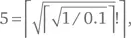
потому что √24 = 4,89, а потолок этого числа равен 5. Поэтому я смогу теперь представить 29 и 30!

Говоря это, я имел в виду просто 30, а не факториал 30, вы понимаете. Пунктуация в математике – такая морока.

Ватсап и Сомс прошли в этой задаче гораздо дальше, и позже мы увидим, чего они в конце концов достигли. Но, прежде чем продолжить эту историю, вы, может быть, захотите проверить, как далеко удастся пройти вам самостоятельно.

«Знак одного» продолжается в главе «Знак одного: часть вторая».

Вспомним, что натуральное число считается составным, если оно может быть получено перемножением двух меньших натуральных чисел, и простым, если оно не может быть получено перемножением двух меньших натуральных чисел и при этом больше 1. Число 1 является исключением: несколько веков назад оно считалось простым, но при таком соглашении разложение числа на простые множители перестает быть единственным. Так, 6 =2 × 3 = 1 × 2 × 3 = 1 × 1 × 2 × 3 и т. д. В наши дни, по этой и другим причинам, 1 считается особым числом. Это число не простое и не составное, это просто единица: натуральное число x , такое, что 1/ x также является натуральным числом. Собственно, 1 – это единственная положительная единица счета.