Иэн Стюарт - Математические головоломки профессора Стюарта

Это общая идея: если процесс деления на квадраты рано или поздно прекращается, значит, отношение сторон прямоугольника выражается рациональным числом. Более того, обратное тоже верно: если отношение сторон прямоугольника рационально, каракули рано или поздно закончатся. Так что «конечные» каракули в точности соответствуют «рациональным прямоугольникам».

Чтобы понять почему, взглянем на числа повнимательнее. По существу, рисунок сообщает нам следующее:

17 – 5 = 12;

12 – 5 = 7;

7 – 5 = 2.

После этого у нас остается прямоугольник 5 × 2 и пора переходить к среднему квадрату:

5 – 2 = 3;

3 – 2 = 1.

Остался прямоугольник 2 × 1, пора переходить к маленькому квадратику:

2 – 1 = 1;

1 – 1 = 0.

Стоп! И дело рано или поздно должно дойти до остановки, потому что все задействованные целые числа положительны и с каждым шагом они делаются все меньше и меньше. Так и должно быть, ведь мы каждый раз либо вычитаем из них что-то, либо оставляем, как есть. А последовательность положительных целых чисел не может уменьшаться до бесконечности. Если вы, к примеру, начнете с миллиона и будете все время уменьшать, то вам придется остановиться не более чем через миллион шагов.

Короче говоря, каракули сообщают нам вот что:

при делении 17 на 5 получается 3 с остатком 2;

при делении 5 на 2 получается 2 с остатком 1;

2 делится на 1 нацело с нулевым остатком,

а процесс останавливается, как только остаток становится равным нулю.

Евклид использовал подобные каракули для решения одной арифметической задачи: поиска наибольшего общего делителя для двух заданных целых чисел. Наибольший общий делитель – это наибольшее целое число, на которое оба заданных числа делятся нацело; его часто обозначают аббревиатурой НОД. К примеру, для чисел 4500 и 840 НОД равен 120.

Меня в школе учили искать НОД таким способом: разложить заданные числа на простые множители и посмотреть, какие множители у них окажутся общими. К примеру, пусть нам надо найти НОД чисел 68 и 20.

Раскладываем то и другое на простые множители:

68 = 2²× 17; 20 = 2²× 5.

НОД равен 2² = 4.

Применимость этого метода ограничена тем, что числа должны быть достаточно небольшими, чтобы их можно было быстро разложить на простые множители. Для более крупных чисел он совершенно неэффективен. Древние греки знали более эффективный способ – процедуру, которой они дали забавное название антифарезис . В данном случае ее применение выглядит так:

68 делим на 20, получаем 3 с остатком 8;

20 делим на 8, получаем 2 с остатком 4;

8 делим на 4, получаем 2 ровно.

Стоп!

Это тот же расчет, что мы проделали для 17 и 5, но теперь все числа вчетверо больше (но делятся они друг на друга столько же раз). Если вы расчертите прямоугольник 68 × 20 каракулями, то картинка получится та же, что и в прошлый раз, только последний маленький квадратик будет иметь размер 4 × 4, а не 1 × 1.

Техническое название этого метода – алгоритм Евклида. Вообще, алгоритм – это рецепт для расчета. Евклид поместил такой рецепт в свои «Начала» и использовал его в качестве основы для теории простых чисел. В символьном виде алгоритм каракулей выглядит так. Возьмем два положительных целых числа m £ n . Начнем с пары ( m, n ) и заменим ее парой ( m, n – m ) в порядке величин, начиная с меньшего: то есть преобразуем

( m, n ) → (min ( m, n – m ), max ( m, n – m )),

где min и max обозначают, соответственно, минимум и максимум. Повторим процедуру. На каждом шаге большее число пары уменьшается, так что в конечном итоге процесс завершается, к примеру, парой (0, h ). Тогда h и есть искомое НОД. Доказательство несложно: любой делитель m и n является также делителем ( n – m ) и наоборот. Поэтому на каждом шаге НОД обоих чисел пары не меняется.

Этот метод по-настоящему эффективен: с его помощью можно вычислять НОД вручную для действительно больших чисел. Чтобы доказать это, вот вам задание. Найдите НОД чисел 44 758 272 401 и 13 164 197 765.

Ответ в главе «Загадки разгаданные».

Насколько эффективен алгоритм Евклида?

Отсекание по одному квадрату за раз проще для теоретических целей, но более компактная форма в терминах деления с остатком лучше подходит для практического использования. При этом вся работа с квадратами одного размера сокращается до одной операции.

Бóльшая часть вычислительных усилий при этом приходится на операцию деления, так что мы можем оценить эффективность алгоритма, подсчитав, сколько раз производится эта операция. Первым этот вопрос исследовал Антуан Рейно, в 1911 г. он доказал, что число операций деления в процедуре поиска НОД составляет максимум m , то есть не превышает меньшего из двух чисел. Это очень грубая оценка, и позже Рейно снизил ее до m /2 + 2, что ненамного лучше. В 1841 г. П. Финк снизил эту оценку до 2 log 2 m + 1, что пропорционально числу десятичных знаков в m . В 1844 г. Габриель Ламе доказал, что число операций деления не более чем в пять раз превосходит число десятичных знаков в m . Так что даже для двух чисел по 100 знаков каждое алгоритм позволяет получить ответ не более чем за 500 шагов. В целом можно сказать, что сделать это так же быстро с использованием простых множителей невозможно.

Что представляет собой наихудший сценарий? Ламе доказал, что алгоритм выполняется медленнее всего в том случае, когда m и n являются последовательными членами ряда Фибоначчи

1 1 2 3 5 8 13 21 34 55 89…,

в котором каждое следующее число представляет собой сумму двух предыдущих. Для этих чисел на каждом шаге от прямоугольника отсекается ровно один квадрат. К примеру, при m = 34, n = 55 получаем

деление 55 на 34 дает 1, остаток 21;

деление 34 на 21 дает 1, остаток 13;

деление 21 на 13 дает 1, остаток 8;

деление 13 на 8 дает 1, остаток 5;

деление 8 на 5 дает 1, остаток 3;

деление 5 на 3 дает 1, остаток 2;

деление 3 на 2 дает 1, остаток 1;

деление 2 на 1 дает 1 ровно.

Необычайно длинный расчет для таких небольших чисел.

Математики проанализировали также среднее число операций деления. При фиксированном n число таких операций, усредненное по всем меньшим m , составляет примерно

где C – так называемая постоянная Портера, равная

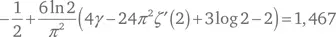
Здесь ζ' (2) – оценка производной от римановой дзета-функции в точке 2, а γ – постоянная Эйлера, равная 0,577. Было бы трудно найти разумную задачу, при решении которой в одной формуле собирается более представительная выборка математических констант. Отношение вычисленного по этой формуле значения к точному ответу стремится к 1 по мере возрастания n .