Иэн Стюарт - Математические головоломки профессора Стюарта

цена банковского кризиса: 10¹² фунтов;

цена одного вулканического дня: 10 8фунтов;

10 12/10 8= 10 4дней = 27 лет.

Этот период представляется мне в высшей степени наглядной величиной: очевидно, что 27 лет – это намного дольше, чем один день. Поэтому я вполне могу осознать, что запрет на полеты должен был бы продолжаться 27 лет, чтобы потери от него сравнялись с экономическим ущербом от банковского кризиса, не обращая внимания на то, что большие числа, участвующие в расчете, не укладываются у меня в голове.

Именно для этого и нужна математика. Не нужно, чтобы вещи укладывалисьу вас в голове: лучше их посчитать.

Я с отвращением бросил газету на стол.

– Послушайте, Сомс… Вы только взгляните на эту нелепую статистику!

Хемлок Сомс хмыкнул и сосредоточился на раскуривании трубки.

– Семьдесят пять процентов кэбменов уверены, что их способности к управлению кэбом выше средних!

Сомс поднял голову.

– Что же в этом нелепого, Ватсап?

– Ну, я… Сомс, но это же просто невозможно! Все они, должно быть, имеют о себе завышенное мнение!

– Почему?

– Потому что среднее должно быть в середине.

Детектив вздохнул.

– Обычное заблуждение, Ватсап.

– Заблуж… что здесь не так?

– Да почти все, Ватсап. Представьте, что 100 человек оценили по шкале от 0 до 10. Если 99 из них получили оценку 10, а один – оценку 0, какое будет среднее?

– Э-э… 990/100… это будет 9,9, Сомс.

– И сколько из них окажется выше среднего?

– Э-э… 99.

– Я же говорю, заблуждение.

Но меня непросто было отвлечь.

– Но все они лишь чуть-чуть превосходят среднее, Сомс, да и данные не слишком типичны.

– Я намеренно выпятил этот эффект, чтобы сделать его более заметным, Ватсап. Любые сдвинутые – асимметричные – данные, как правило, ведут себя сходным образом. Предположим, к примеру, что большинство кэбменов достаточно компетентны, значительное меньшинство ужасны, а несколько человек – очень немного – превосходны в своем деле. Кто из кэбменов в таком случае окажется выше среднего?

– Ну… дурные утянут среднее значение вниз, и превосходных не хватит, чтобы их уравновесить… Господи! Все компетентные и превосходные кэбмены окажутся выше среднего!

– В самом деле, – отозвался Сомс. Он быстро набросал на каком-то случайном листе диаграмму. – С этими данными, которые более реалистичны, среднее значение равно 6,25, и 60 % кэбменов оказываются выше него.

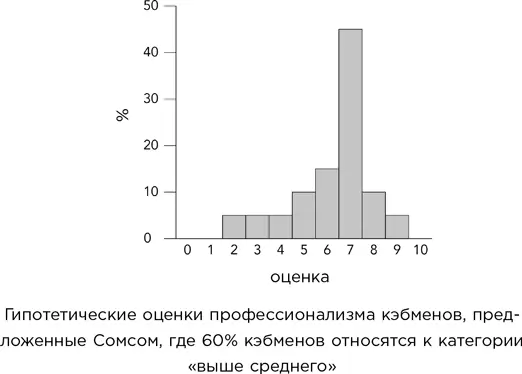
– Так что статья в Manchester Mirrograph ошибочна? – поинтересовался я.

– Вас это удивляет, Ватсап? Откровенно говоря, у них редко попадаются полностью правдивые статьи. Но здесь журналист угодил в обычную ловушку. Он спутал среднее значение с медианным, которое определяется как значение, для которого половина оценок находится выше, а половина – ниже. Эти две величины часто не совпадают.

– Получается, что 75 % кэбменов ни при каких обстоятельствах не могут иметь уровень выше медианного?

– Только если число кэбменов равно нулю.

– Но при этом 75 % кэбменов в принципе может иметь уровень выше среднего?

– Да.

– И это не означало бы, что у них всех завышенное самомнение?

Сомс снова вздохнул.

– А вот это, мой дорогой Ватсап, совсем другой коленкор, и даже другого цвета. Существует распространенная форма когнитивной ошибки, которую называют иллюзорным превосходством. Многие воображают себя выше других, даже если это на самом деле не так. Почти все мы страдаем этим заблуждением, за исключением, естественно, меня. В прошлом месяце журнал Quantitative Phrenology and Cognition [26] Вымышленное название, которое можно перевести как «Количественная френология и познание». Френология – псевдонаука о связи психики человека с поверхностью его черепа. – Прим. ред. написал, что 69 % шведских кэбменов считают свои способности выше медианных . Это точно иллюзия, даже не сомневайтесь.

Реальные современные данные см. в главе «Загадки разгаданные».

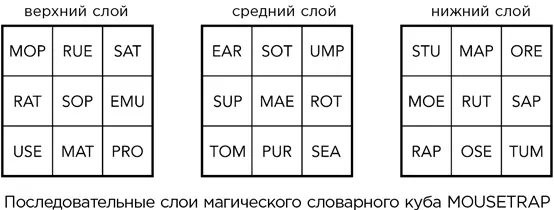
Джереми Фаррелл придумал магический словарный куб, который подчиняется тем же правилам, что и его магические квадраты. В кубе задействовано слово MOUSETRAP (мышеловка), а буквам присвоены следующие магические значения: M = 0, O = 0, U = 2, S = 6, E = 9, T = 18, R = 3, A = 1, P = 0. Некоторые из слов куба представляют собой личные имена, а некоторые используются очень редко. К примеру, OSE – это имя какого-то демона, а также название мест в Японии, Нигерии, Польше, Норвегии и на острове Скай. Тем не менее поразительно уже то, что такую вещь в принципе можно сделать.

Специалисты по теории чисел, занятые поисками больших простых чисел, часто рассматривают числа вида k 2 n + 1 для какого-то выбранного k при разных n . Пробные расчеты позволяют предположить, что для большинства значений k среди этих чисел встречается по крайней мере одно простое число, часто больше. К примеру, если k = 1, то 1 × 2 n + 1 является простым для n = 2, 4, 8. Если k = 3, то 3 × 2 n + 1 простое при n = 1, 2, 5, 6, 8, 12. Если k = 5, то 5 × 2 n + 1 простое при n = 1, 3, 7. (В общем случае мы можем разделить k на 2 столько раз, сколько нужно, чтобы получить нечетное число, а все двойки включить в 2n. Поэтому можно смело считать k нечетным, не теряя общности. К примеру, 24 × 2 n = 3 × 23× 2 n = 3 × 2 n+ 3.)

Соблазнительно предположить, что для любого k ³≥2 существует по крайней мере одно простое число вида k 2 n + 1. Однако в 1960 г. Вацлав Серпинский доказал, что существует бесконечно много нечетных k , для которых все числа вида k 2 n + 1 являются составными. Эти числа получили название чисел Серпинского.

В 1992 г. Джон Селфридж доказал, что 78 557 – число Серпинского; он показал, что все числа вида 78 557 × 2 n + 1 делятся по крайней мере на одно из чисел 3, 5, 7, 13, 19, 37, 73. Говорят, что эти числа образуют покрывающее множество. Приведем первые десять известных чисел Серпинского:

78 557 271 129 271 577 322 523 327 739

482 719 575 041 603 713 903 983 934 909

Считается, что 78 557 – наименьшее число Серпинского, но пока этот факт никем не доказан и не опровергнут. В 2002 г. на сайте www.seventeenorbust.comбыл организован поиск простых чисел вида k 2 n + 1, существование которых доказывало бы, что k не является числом Серпинского. Когда поиск только начинался, у математиков было 17 кандидатов на роль чисел Серпинского, не превышающих 78 557, но постепенно они были ликвидированы, так что осталось только шесть: 10 223, 21 181, 22 699, 24 737, 55 459 и 67 607. Попутно в рамках проекта было найдено несколько очень больших простых чисел.