Иэн Стюарт - Математические головоломки профессора Стюарта

Джеймс Джозеф Силвестер – английский математик, работавший с Артуром Кейли, в частности в области теории матриц и теории инвариант. Всю жизнь он очень интересовался поэзией и часто вставлял стихотворные цитаты в свои математические научные статьи. В 1841 г. он переехал в США, но вскоре вернулся обратно. В 1877 г. он вновь пересек Атлантику, занял место первого профессора математики в Университете Джона Хопкинса и основал American Journal of Mathematics , издающийся с немалым успехом и сегодня. Он вернулся в Англию в 1883 г.

Изначально его звали просто Джеймс Джозеф. Когда его старший брат эмигрировал в США, в офисе иммиграционной службы ему сказали, что у каждого должно быть по три имени: два имени и фамилия. По какой-то причине брат взял себе новую фамилию – Силвестер, сделав прежнюю вторым именем. Джеймс Джозеф последовал примеру брата.

При ограблении величественного особняка лорда Баффлхэма из сейфа похитили несколько изумрудов и рубинов. Сомс, которого пригласили расследовать дело, быстро заподозрил двух гостей – леди Изабеллу Никетт и баронессу Руби Робхэм. Та и другая испытывали серьезные материальные трудности и, без сомнения, не устояли перед искушением. Но где доказательства?

Обе дамы признались, что у них есть кое-какие драгоценности, но утверждали, что это их собственность. Сомсу пока не удалось убедить инспектора Роулейда получить ордер на обыск в аристократических домах, хотя это могло бы разрешить все проблемы; пока же он не мог заглянуть в шкатулки с драгоценностями означенных дам.

– Дело, – сказал Сомс, – определяется тем, сколько драгоценностей имеют наши две дамы. Если их число совпадает с числом похищенных вещей, мы получаем последнее необходимое доказательство. Роулейд готов запросить ордер на обыск, но только если мы сможем снабдить его этими двумя числами.

– Изабелла заявила, что у нее имеются только изумруды, – пробормотал я вполголоса. – А Руби говорит, что у нее только рубины.

– В самом деле. Я уверен, что оба эти заявления правдивы. Далее, из показаний лакея следует, что число тех и других драгоценностей лежит в интервале от 2 до 101 включительно.

– Кухарка не настроена болтать о хозяйках, – заметил я. – Но мне удалось убедить ее открыть произведение этих двух чисел.

– А дворецкий, тоже неболтливый, но убежденный аргументом в виде десяти золотых соверенов, назвал мне их сумму, – отозвался Сомс.

– Значит, мы можем, решив квадратное уравнение, найти оба числа! – возбужденно воскликнул я.

– Разумеется, хотя мы не будем знать, какое из чисел относится к изумрудам, а какое – к рубинам, – протянул Сомс. – Данные симметричны. Но любого совпадения будет достаточно, чтобы инспектор Роулейд получил ордер на обыск, а там все, я не сомневаюсь, найдется.

– Если вы назовете мне произведение, – сказал я, – то я смогу решить уравнение.

– Ах, мой дорогой Ватсап, вам не достает утонченности, – критически заметил Сомс. – Дайте посмотреть, нельзя ли вывести числа без этого… Так, знаете, чему они равны?

– Нет.

– Я так и знал, – заявил Сомс, к моему раздражению. Если знал, зачем спрашивать? Неожиданно меня осенило.

– Теперь я тоже знаю эти числа, – объявил я.

– В таком случае я тоже их знаю, Ватсап.

Какие это два числа? Ответ см. в главе «Загадки разгаданные».

В настоящее время нам известно десятичное значение π с точностью до 12 100 000 000 050 знаков; соответствующий расчет провел в 2013 г. Сигеру Кондо, и потребовалось ему на это 94 дня. На самом деле никому нет дела до того, какой получен ответ, но известно, что замечательные рекордные усилия такого рода нередко приводят к новым озарениям, а также являются хорошим способом проверки новых суперкомпьютеров. Одно из самых забавных открытий состоит в том, что можно вычислять отдельные цифры десятичной записи π без нахождения всех предыдущих цифр. Однако в настоящее время мы можем это делать только в шестнадцатеричной нотации, то есть в системе счисления с основанием 16, из которой можно без труда получить цифры в системах счисления с основаниями 8, 4 и 2 (двоичной). Эта идея работает и для других констант, не только для π, а также для троичной системы счисления, но систематической теории на этот счет пока нет. Для десятичной нотации, то есть для системы счисления с основанием 10, ничего подобного не известно.

Первоначальное открытие, формула ББП (Бейли – Боруэйна – Плаффа), изложена ниже; вы найдете ее также в «Кабинете…» на с. 264. Это бесконечный ряд, при помощи которого можно вычислить конкретный шестнадцатеричный знак числа π, не вычисляя при этом предыдущих его знаков. Так что мы можем быть уверены, что квадриллионный двоичный знак числа π – нуль, благодаря проекту PiHex; пройдя еще дальше, скажем, что двухквадриллионный двоичный знак π также равен 0, благодаря расчету, проведенному одним из сотрудников компании Yahoo! и занявшему 23 дня. Несмотря на все наши познания, для того чтобы найти предыдущий знак, потребовался бы еще один столь же длительный расчет.

В 2011 г. Дэвид Бейли, Джонатан Боруэйн, Эндрю Маттинли и Гленн Уайтвик составили обзорное исследование этого вопроса [27] David Bailey, Jonathan Borwein, Andrew Mattingly, and Glenn Wightwick. The computation of previously inaccessible digits of π2 and Catalan's constant, Notices of the American Mathematical Society 60 (2013) 844–854. . Авторы описали способ нахождения знаков числа π² в системе счисления с основанием 64, знаков числа π² в системе счисления с основанием 729 и знаков числа, известного как постоянная Каталана, в системе счисления с основанием 4096, начиная с 10-триллионной позиции.

История начинается с последовательности, известной еще Эйлеру:

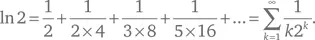
Благодаря степеням двойки, которые здесь фигурируют, этот ряд можно преобразовать в метод вычисления конкретных двоичных знаков ln 2. По мере роста номера знака вычисления остаются реализуемыми, хотя и занимают гораздо больше времени.

Формула ББП выглядит так:

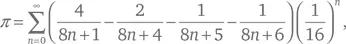
и степени 16 делают возможным вычисление конкретных шестнадцатеричных знаков числа π. Поскольку 16 = 2 4, ряд можно использовать также для вычисления двоичных знаков.