Иэн Стюарт - Математические головоломки профессора Стюарта

У квадратичных вычетов множество самых разных применений. Один из моих любимых примеров – проектирование концертных залов. Музыка, отражаясь от плоского потолка, дает явственное эхо, которое искажает звук и вообще мешает слушать. С другой стороны, звукопоглощающий потолок делает звучание мертвым и смазанным. Для хорошей акустики звук должен отражаться, но в виде рассеянного отзвука, а не резкого эха. Поэтому архитекторы встраивают в потолок специальные рассеиватели. Вопрос в том, какой они должны быть формы.

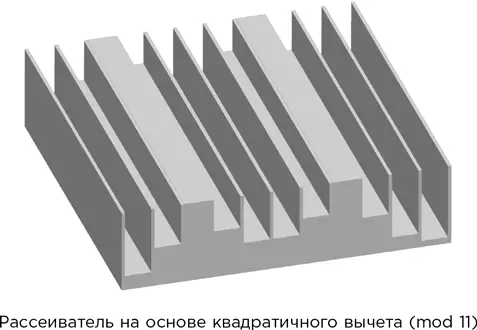
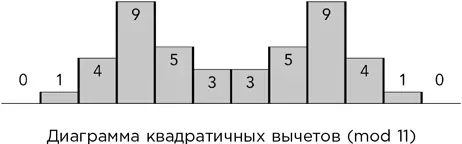
В 1975 г. Манфред Шрёдер изобрел рассеиватель, состоящий из серии параллельных борозд, глубина которых выводится из последовательности квадратичных вычетов для некоего простого модуля. Возьмем, к примеру, простое число 11. Мы только что видели, что квадраты чисел от 0 до 10 по модулю 11 равны:

0 1 4 9 5 3 3 5 9 4 1,

и далее, для более крупных чисел, эта последовательность повторяется периодически. Она симметрична относительно середины, промежутка между двумя тройками, потому что x ² = (– x )² по любому простому модулю. Сравним рисунок ниже – на нем эти числа показаны в виде прямоугольников – с формой рассеивателя на предыдущем рисунке. Обратите внимание: в данном случае глубина выемок получается путем вычитания вычетов из какой-то постоянной величины. Это не оказывает серьезного влияния на основной математический смысл.

Что такого особого в квадратичных вычетах? Одна из характеристик звуковой волны – ее частота: сколько волн приходит в ухо каждую секунду. Высокие частоты дают высокие звуки, низкие частоты – низкие звуки. Еще одна характеристика, связанная с частотой, – длина волны: расстояние между последовательными пиками. Высокочастотные волны короче, низкочастотные – длиннее. Колебания с заданной длиной волны резонируют с пустотами в поверхности, размеры которых близки к длине их волны. Так что волны разных частот по-разному реагируют на столкновение с поверхностью.

Рассеиватель на основе квадратичных вычетов обладает восхитительным математическим свойством: волны различных частот взаимодействуют с ним одинаково. Технически это означает, что преобразование Фурье постоянно на некотором диапазоне частот. Шрёдер указал на одно важное следствие: такая форма рассеивает звуковые волны многих разных частот одинаково. На практике ширина бороздок выбирается так, чтобы избежать диапазона волн, доступных для человеческого уха, а их длина кратна с определенным коэффициентом последовательности квадратичных вычетов, связанных с шириной.

Когда бороздки параллельны, как на рисунке, звук рассеивается в стороны, под прямым углом к бороздкам. Существует двумерный аналог этой системы – квадратное поле со стержнями, тоже рассчитанными на основе квадратичных вычетов, – который рассеивает звук равномерно во всех направлениях. Такие рассеиватели часто можно найти в звукозаписывающих студиях, где они помогают улучшить звуковой баланс и избавиться от лишних шумов.

Так что хотя Эйлер и Гаусс понятия не имели, для чего когда-нибудь будет использовано их изобретение и будет ли оно использовано хоть для чего-то, оно нередко играет принципиально важную роль (неявно, где-то за сценой), когда вы слушаете записанную музыку, будь то классика, джаз, кантри, рок, хип-хоп, кроссовер-трэш металлика – все что угодно.

Дополнительную информацию см. в главе «Загадки разгаданные».

– Расследование преступления часто сравнивают со складыванием пазла, – заметил Сомс неожиданно, без всякого повода. Если, конечно, не считать поводом голубоватую струйку дыма из его трубки, за которую так и хотелось потянуть. Дым окутывал его голову настоящим облаком.

– Уместное сравнение! – отозвался я, поднимая голову от газеты.

Он хитро улыбнулся.

– Вовсе нет, Ватсап. Напротив, очень неудачное. Расследуя преступление, мы не знаем, какими могут быть эти кусочки, и не можем даже сказать, все ли они находятся в нашем распоряжении. Не зная, что за головоломка у нас в руках, как можем мы быть уверены в ответе?

– Право, Сомс, ведь это становится очевидным, когда достаточное число известных элементов складывается в единый элегантный узор.

Он вздохнул.

– Ах, но кусочков может быть так много, Ватсап! И разных узоров, которые они могут образовать, тоже. Чтобы решить, который из них правильный, нужно обладать определенным… je ne sais quoi [29] Буквально «сам не знаю что» (фр.); применительно к искусству означает неуловимую, невыразимую красоту. – Прим. ред. . Но я не знаю, чем именно.

В этот момент раздался стук в дверь, и в гостиную буквально ворвалась какая-то женщина.

– Беатрис! – воскликнул я.

– О, Джон! Ее украли! – и она, рыдая, бросилась в мои объятия. Я постарался утешить ее как мог, хотя мое сердце, признаюсь, пустилось вскачь.

Через некоторое время она успокоилась.

– Пожалуйста, помогите мне, мистер Сомс! Это рубиновая подвеска, она досталась мне от матери. Я везде искала ее сегодня утром, но она исчезла!

– Не расстраивайтесь, дорогая, – сказал я, похлопывая Беатрис по плечу. – Мы с Сомсом поймаем вора и вернем вашу драгоценность.

– Вы приехали в кэбе? – поинтересовался Сомс.

– Да. Он ждет снаружи.

– Тогда не будем терять времени и обследуем место преступления.

Через полчаса ползания по полу, взятия образцов пыли из углов в нескольких комнатах и внимательного осмотра порога и клумб под окнами Сомс покачал головой.

– Никаких следов взлома и проникновения, мисс Шипшер. А вот на вашей шкатулке с украшениями есть маленькие царапины. Свежие и не ваши, поскольку сделаны левшой, – он поставил шкатулку на место. – Бывали ли в доме в последнее время посторонние? Может быть, торговцы?

– Нет… Ох! Плиточники!

Два человека, назвавшиеся плиточниками, стучались с черного хода и предлагали обновить ванную комнату в доме.

– Это новая мода, мистер Сомс. Белые квадратные плитки, среди которых из плиток более сложной формы выложен синий узор. У Димвортов ванную отделали таким образом в прошлом месяце, и отец… – ее голос сорвался, Беатрис расстроенно замолчала, чуть не плача. Я взял ее за руку.

– Часто вы нанимаете незнакомых рабочих, которые стучатся к вам с черного хода? – поинтересовался Сомс.

– Что вы, нет, мистер Сомс. Обычно мы стали бы разговаривать только с солидной фирмой. Но у них у всех полно заказов и все расписано на несколько месяцев вперед. А эти рабочие казались честными, достойными людьми.