Иэн Стюарт - Математические головоломки профессора Стюарта

«Для любого ε > 0 существует лишь конечное число троек положительных целых чисел, не имеющих общих делителей и удовлетворяющих уравнению a + b = c , таких, что с > d 1 + ε, где d обозначает произведение различных простых делителей abc» .

Это и есть гипотеза ABC. Если бы ее удалось доказать, многие глубокие и сложные теоремы, доказанные в последние десятилетия с огромными усилиями и самыми хитроумными методами, оказались бы ее прямыми следствиями и получили более простые доказательства. Более того, все эти доказательства были бы очень похожи между собой: провести несложную рутинную подготовку, а затем применить « теорему ABC» , как она бы тогда называлась. Эндрю Грэнвилл и Томас Такер [35] Andrew Granville and Thomas Tucker. It's as easy as abc, Notices of the American Mathematical Society 49 (2002) 1224–1231. пишут, что разрешение этой гипотезы произвело бы «…необычайный эффект на наши представления о теории чисел. Доказательство или опровержение ее было бы ошеломительным».

Но вернемся к Мотидзуки, уважаемому специалисту по теории чисел с солидным багажом исследований. В 2012 г. он изложил предполагаемое доказательство гипотезы ABC в серии из четырех препринтов – статей, не представленных пока для официальной публикации. Вопреки его намерениям эта публикация привлекла внимание средств массовой информации, хотя с его стороны, конечно, было наивно полагать, что подобного исхода удастся избежать. В настоящее время специалисты проверяют 500 или около того страниц принципиально новой математики, из которых состоит доказательство. Это занимает много времени и усилий, потому что идеи в нем формализованны, сложны и необычны; однако никто не отвергает доказательство только по этой причине. Одна ошибка уже найдена, но Мотидзуки заявил, что она не портит доказательство. Он продолжает публиковать отчеты по ходу проверки, а эксперты продолжают свою работу.

Восемь одинаковых кубов, плотно составленных гранями, образуют куб вдвое большего размера. Восемь кубов можно составить и так, чтобы они образовали «кольцо» – объемную фигуру с отверстием, топологически – тор.

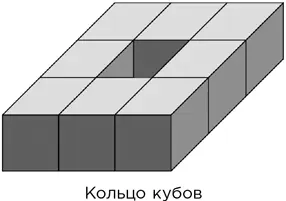
Приложив некоторые усилия, можно проделать то же самое с тремя другими правильными многогранниками: октаэдром, додекаэдром и икосаэдром. Во всех четырех случаях многогранники совершенно правильные и стыкуются друг с другом в точности: это очевидно для кубов и прямо следует из симметрии для трех остальных многогранников.

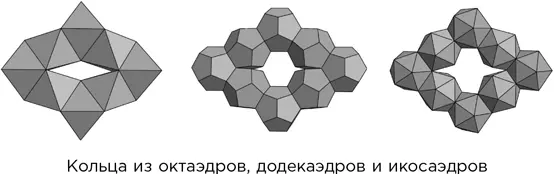
Однако всего существует пять правильных многогранников, и для одного из них – тетраэдра – этот метод не работает. Поэтому в 1957 г. Гуго Штейнгауз задал вопрос о том, можно ли склеить некоторое количество одинаковых правильных тетраэдров гранью к грани так, чтобы они образовали замкнутое кольцо. Ответ на его вопрос был дан годом позже, когда С. Сверчковский доказал, что подобная комбинация невозможна. Тетраэдр – особый многогранник.

Однако в 2013 г. Майкл Элгерсма и Стэн Вэгон открыли красивое восьмисторонне-симметричное кольцо из 48 тетраэдров. Неужели Сверчковский ошибся?

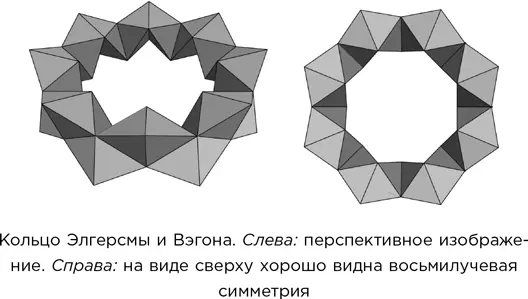
Вовсе нет, как объяснили Элгерсма и Вэгон в своей статье, посвященной этому открытию. Если изготовить эту комбинацию из правильных тетраэдров, останется небольшой разрыв. Этот разрыв можно закрыть, если удлинить ребра, показанные на рисунке жирными линиями, с 1 до 1,00274, примерно на одну пятисотую, чего человеческий глаз заметить не в состоянии.

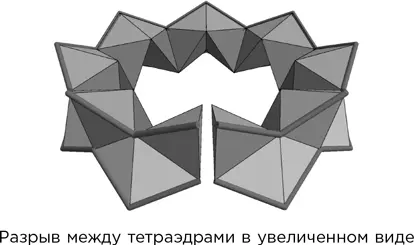
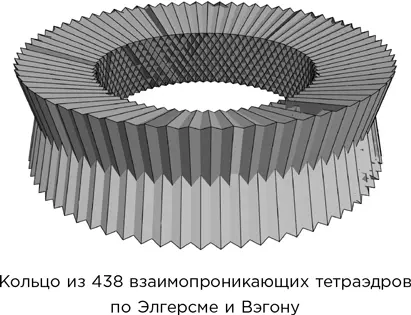
Сверчковский спрашивал: если взять много тетраэдров и составить их в кольцо с разрывом, то насколько маленьким может оказаться этот разрыв? Можно ли сделать его сколь угодно маленьким по отношению к размеру одного тетраэдра за счет использования достаточно большого их числа? Ответ на этот вопрос неизвестен до сих пор, при условии что тетраэдры не могут пересекаться друг с другом, однако Элгерсма и Вэгон доказали, что, если разрешить взаимопроникновение, ответ должен быть положительным. К примеру, 438 тетраэдров оставляют разрыв, составляющий примерно одну десятитысячную длины ребра.

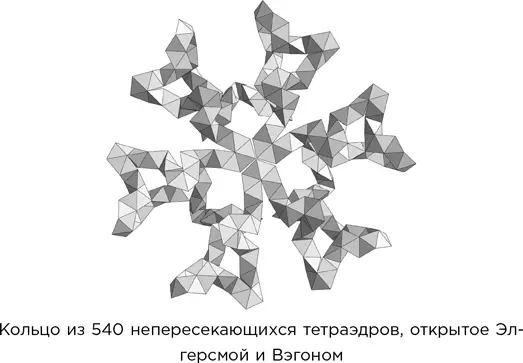
Авторы предположили, что ответ должен быть положительным, даже если тетраэдрам не разрешено пересекаться, но конструкции при этом должны возникать значительно более сложные. В доказательство они нашли серию колец со все уменьшающимися разрывами. Нынешний рекорд, открытый в 2014 г., представляет собой почти замкнутое кольцо из 540 непересекающихся тетраэдров с разрывом 5 × 10 –18.

Дополнительную информацию см. в главе «Загадки разгаданные».

Эта математическая загадка оставалась нерешенной больше 100 лет. Правда ли, что любая простая (без самопересечений) замкнутая кривая на плоскости содержит четыре точки, представляющие собой углы квадрата с ненулевой стороной?

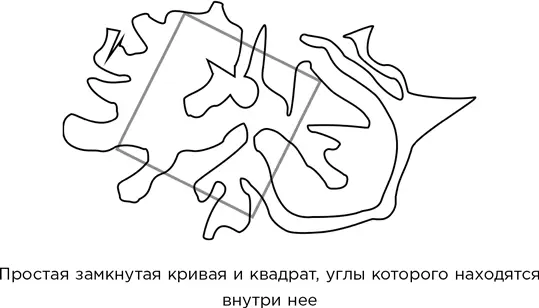
Под «кривой» здесь подразумевается непрерывная линия без разрывов, не обязательно гладкая. Она может иметь острые углы и вообще может быть бесконечно извилистой. Мы настаиваем на ненулевой стороне квадрата, чтобы избежать тривиального ответа, когда одна и та же точка представляет все четыре угла.

Первое печатное упоминание о задаче с квадратным колышком появилось в 1911 г. в ходе конференции на семинаре, который проводил Отто Тёплиц; судя по всему, было обещано доказательство. Однако никакого доказательства опубликовано не было. В 1913 г. Арнольд Эмч доказал, что это утверждение верно для гладких выпуклых кривых, но добавил, что услышал о задаче не от Тёплица, а от Обри Кемпнера. Это утверждение было доказано для выпуклых кривых, аналитических кривых (определяемых сходящимися степенными рядами), достаточно гладких кривых, кривых с симметрией, звездчатых дважды дифференцируемых кривых, пересекающих любую окружность в четырех точках…

В общем, вы поняли. Множество технических гипотез, но никакого общего доказательства и никаких контрпримеров. Может быть, да, может быть, нет. Кто знает?