Иэн Стюарт - Математические головоломки профессора Стюарта

– Все эти силы изменяются во времени, – заметил я.

Он кивнул.

– Важно здесь то, что специалисты по механике называют моментом каждой силы, – степень, в которой она поворачивает лодку вокруг какой-то выбранной точки. Находят его, как вы помните из истории с палимпсестом Архимеда, перемножением силы на расстояние от точки ее приложения по перпендикуляру до этой точки.

Настала моя очередь кивнуть. Я был уверен, что припоминаю что-то в этом роде.

– Я отмечаю положение ближайшего к корме весла точкой. Это и будет наша выбранная точка. Далее, сила P имеет момент Pd относительно точки, в которой крепление уключины весла пересекается с центральной продольной осью лодки, если это весло расположено на левой стороне. Но если оно располагается справа, момент будет равен – Pd , поскольку сила при этом закручивает лодку в противоположном направлении. Обратите внимание: эти моменты для всех четырех весел на одном борту лодки одинаковы. Следовательно, суммарный момент всех восьми весел равен 4 Pd – 4 Pd , то есть 0.

– Вращающие силы уравновешивают друг друга!

– Для продольных составляющих P – да, уравновешивают. Однако момент силы R у каждого весла свой, поскольку зависит от расстояния x между этим веслом и крайним кормовым. Если говорить конкретно, этот момент равен Rx . Если расстояние между соседними веслами везде одинаково и равно c , то x принимает значения

0 cR 2 cR 3 cR 4 cR 5 cR 6 cR 7 cR

по мере продвижения от кормы к носу. Поэтому суммарный момент равен

± 0 ± cR ± 2 cR ± 3 cR ± 4 cR ± 5 cR ± 6 cR ± 7 cR,

где ставится знак плюс для весел левого борта и знак минус – для весел правого борта.

– Почему?

– Силы на левой стороне поворачивают лодку по часовой стрелке, Ватсап, а силы по правой стороне – против. Можно упростить это выражение до (± 0 ± 1 ± 2 ± 3 ± 4 ± 5 ± 6 ± 7) cR, где последовательность плюсов и минусов соответствует последовательности сторон, на которые смотрят весла.

– А теперь рассмотрим стандартное расположение весел на спортивной распашной восьмерке. Последовательность знаков здесь такова:

+ – + – + – + –,

так что суммарный крутящий момент равен

(0–1 + 2–3 + 4–5 + 6–7) cR = –4 cR .

В первой фазе гребка R направлена внутрь, но, когда весло начинает уходить назад, направление R меняется, она начинает действовать наружу. Поэтому лодка в ходе гребка сначала поворачивается в одном направлении, затем в другом, то есть вихляет на ходу. Рулевой должен при помощи руля корректировать ход лодки, а это, как я уже сказал, порождает сопротивление.

– А что в немецком варианте? Здесь суммарный крутящий момент равен

(0–1 + 2–3 – 4 + 5–6 + 7) cR = 0,

какими бы ни были c и R . Так что лодка в этом варианте не склонна вилять.

– А у итальянцев? – воскликнул я. – О, дайте мне попробовать! Суммарный крутящий момент равен

(0–1–2 + 3 + 4–5–6 + 7) cR = 0.

Тоже! Как замечательно!

– Вот именно, – отозвался Сомс. – А теперь, Ватсап, вопрос для вашего живого ума. Являются ли немецкий и итальянский варианты – или их зеркальные отражения, которые ничем, в сущности, от них не отличаются, – единственными способами обнулить вращающие силы? – должно быть, он заметил выражение моего лица, поскольку добавил: – Вопрос сводится к разделению чисел от 0 до 7 на две группы по четыре, каждая из которых при сложении даст одну и ту же сумму. А именно 14, поскольку все эти числа в сумме дают 28.

Ответ, а также результат гонки Оксфорд – Кембридж 1877 г. см. в главе «Загадки разгаданные».

Эта старая головоломка – моя любимая, она никогда не надоедает. Это увлекательное занятие, где маленькая математическая догадка могла бы избавить нас от невероятного количества напрасных усилий. Плюс к тому она нужна мне в качестве подготовки к следующей теме.

В 1880 г. нью-йоркский почтмейстер по имени Ной Палмер Чепмэн предложил головоломку, которую он назвал «драгоценной», а дантист Чарльз Певи предложил денежный приз за ее решение. Головоломка ненадолго вошла в моду, но никто не сумел выиграть приз, так что ажиотаж быстро спал. Американский составитель головоломок Сэм Лойд [34] Это не опечатка: Лойд действительно писал свою фамилию с одной «Л». – Прим. авт. утверждал, что именно он ввел моду на эту головоломку в 1870-е гг., но на самом деле все, что он сделал, – это написал о ней в 1896 г. и предложил приз в $1000 за решение, что на время воскресило интерес к полузабытой игре.

Головоломка «пятнашки» (ее также называют игрой в «15» и «загадочным квадратом») начинается с 15 подвижных квадратиков, пронумерованных числами от 1 до 15 и расставленных в форме квадрата с одним пустым квадратиком в правом нижнем углу. Квадратики расставлены в порядке возрастания, за исключением номеров 14 и 15. Задача играющего – поменять местами квадратики 14 и 15, сохранив положение остальных квадратиков неизменным. Делать это нужно сдвиганием любого из соседних квадратиков на пустое место, причем повторять эту операцию можно сколько угодно.

По мере того как вы сдвигаете все больше и больше квадратиков, номера перепутываются. Но если вы будете действовать аккуратно, вы сможете вновь их распутать. Легко предположить, что при достаточной сообразительности можно получить любое, абсолютно произвольное расположение квадратиков.

Лойд с радостью предложил такой щедрый по тем временам приз, поскольку был уверен, что платить не придется. В игре существует 16! потенциально возможных перестановок (15 нумерованных квадратиков плюс один пустой). Вопрос в следующем: какие из этих вариантов можно получить при помощи серии разрешенных ходов? В 1879 г. Уильям Джонсон и Уильям Стори доказали, что ответ состоит в том, что получить можно ровно половину вариантов; причем (так мы и знали, не правда ли?) вариант, который нужен для получения приза, относится к другой половине. «Пятнашка» нерешаема. Но люди в большинстве своем этого не знали.

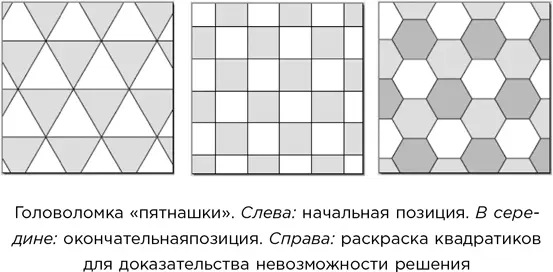
Для доказательства невозможности решения нужно раскрасить квадратики под шахматную доску, как на правом рисунке. Сдвиг любого квадратика, по существу, меняет его местами с пустым квадратиком, и всякий раз при этом меняется цвет, связанный с пустым квадратиком. Поскольку в результате пустой квадратик должен вернуться на свое первоначальное место, число шагов должно быть четным. Вообще, любая расстановка может быть получена путем серии обменов, но некоторые комбинации требуют четного числа обменов, а некоторые – нечетного.