Иэн Стюарт - Математические головоломки профессора Стюарта

– Архимед был настолько великим математиком, что сумел найти логически строгое геометрическое доказательство этих фактов, которое включил в книгу «О шаре и цилиндре». Там он использовал сложный метод доказательства, известный в настоящее время как метод исчерпывания. С этим методом, однако, связаны некоторые сложности, одна из которых состоит в том, что нужно заранее знать точный ответ, верность которого вы и будете доказывать. Поэтому для ученых долгое время было загадкой: откуда Архимед узнал, каким должен быть ответ?

– Понятно, – сказал я. – А в этом давным-давно утерянном документе объясняется, как он это сделал.

– Именно. Замечательно, что метод Архимеда – это почти предвидение – в данном конкретном случае – интегрального исчисления Исаака Ньютона и Готфрида Лейбница, разработанного на 2000 лет позже. Но, как хорошо знал Архимед, идеям, использованным им в «Методе», недостает строгости. Отсюда и метод исчерпывания, к которому ему пришлось прибегнуть… Совершенно иной подход.

– Так как же он это сделал? – спросил я.

Сомс тщательно изучил палимпсест через увеличительное стекло.

– Греческий язык здесь не совсем классический и местами плохо читается, но для такого опытного лингвиста, как я, это не представляет серьезной трудности. Показывал я вам свой памфлет о расшифровке неизвестных древних текстов Средиземноморья? Напомните, чтобы показал.

Судя по всему, Архимед начал с шара, конуса и цилиндра подходящих размеров. Затем он представил тончайший срез каждой из этих фигур и представил, что эти срезы можно взвешивать: срез шара и срез конуса на весах с одной стороны, срез цилиндра – с другой. Если расстояния подобраны правильно, то массы совпадут в точности. А поскольку масса пропорциональна объему, то и объемы фигур связаны по закону рычага.

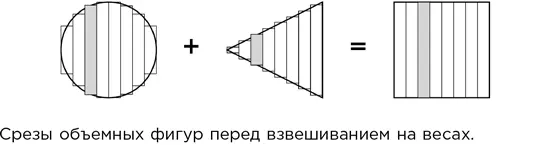
– Э-э… Напомните мне, пожалуйста, этот закон, – сказал я. – Не могу сказать, почему, но его не было в учебной программе медицинской школы.

– А должен был бы быть, – отозвался Сомс. – Он очень пригодился бы при работе с вывихнутыми суставами. Ну, не важно. Закон этот, открытый и доказанный Архимедом, утверждает, что крутящее действие, или момент, заданной массы на заданном расстоянии равен произведению массы на расстояние. Чтобы массы уравновесились, суммарный момент по часовой стрелке должен равняться суммарному моменту против часовой стрелки. Или, при соответствующей расстановке знаков плюс и минус, полный суммарный момент системы должен быть равен нулю.

– Э-э…

– Масса на заданном расстоянии уравновесит половинную массу на вдвое большем расстоянии, если, конечно, она находится на другом плече весов .

– Понятно.

– Подозреваю, что нет, но позвольте мне продолжить. Разбив объемные тела на бесконечное количество бесконечно тонких ломтиков и развесив их нужным образом на своих весах, Архимед сумел сосредоточить всю массу шара и конуса в одной точке. Ломтики цилиндра, которые представляют собой одинаковые круги, размещаются на разных расстояниях; все вместе они составляют первоначальный цилиндр. Зная, что объем конуса (а значит, и его масса) составляет одну треть от соответствующего параметра цилиндра, Архимед смог решить получившееся «уравнение» для объема шара.

– Поразительно, – сказал я. – Мне это все представляется достаточно убедительным.

– Но не математику калибра Архимеда, – возразил Сомс. – Если ломтики имеют конечную толщину, в ходе процедуры возникнут небольшие, но неизбежные ошибки. Но если сделать ломтики нулевой толщины, то и масса у них окажется нулевой. Бессмысленно говорить о единственной точке равновесия, когда все задействованные массы равны нулю.

Я начал понимать сложности, связанные с описанной процедурой.

– Но ведь чем тоньше становятся ломтики, тем меньше, наверное, становятся ошибки? – рискнул я предположить.

– Это так, Ватсап, вы правы. И современный подход к интегральному исчислению превращает это утверждение в доказательство того, что процесс такого рода приводит к разумным ответам. Однако Архимеду эти идеи были неизвестны. Так что он воспользовался нестрогим методом, чтобы найти верный ответ, и это позволило ему прибегнуть к методу исчерпывания, чтобы доказать правильность ответа.

– Поразительно, – вновь сказал я. – Мы должны опубликовать палимпсест.

Сомс покачал головой.

– И рисковать навлечь на себя гнев картонариев? Я слишком высоко ценю наши с вами жизни, чтобы привлекать к себе их внимание.

– Что же нам делать?

– Мы должны поместить рукопись в безопасное место. Не вернуть обратно в библиотеку, ибо там, должно быть, уже заметили ее исчезновение и успели расставить множество хитрых ловушек. Я спрячу его в какой-нибудь другой научной библиотеке. Нет, не спрашивайте, в какой именно! Может быть, когда-нибудь позже, когда времена будут менее тревожные и влияние тайных обществ ослабнет, его найдут заново. А до той поры мы должны удовлетвориться тем, что познакомились с методом великого геометра, хотя и не смогли открыть его миру.

Он ненадолго остановился.

– Я уже рассказал вам о формулах для площади поверхности и объема шара. А вот небольшая и несложная задачка, которая может вас позабавить. Каким должен быть радиус шара в метрах, чтобы площадь его поверхности в квадратных метрах в точности равнялась его же объему в кубических метрах?

– Понятия не имею, – признался я.

– Так выясните, чего ж вы ждете! – воскликнул он.

Подлинную историю архимедова палимпсеста и ответ на загадку Сомса см. в главе «Загадки разгаданные».

Сумма четырех квадратов, как и многие другие математические загадки, имеет давнюю историю. Греческий математик Диофант, чья «Арифметика» примерно 20 г. н. э. была первым учебником, в котором использовалась некая система алгебраических обозначений, задал вопрос, является ли каждое положительное целое число суммой четырех полных квадратов (0 разрешен). Несложно проверить это утверждение экспериментально для небольших чисел, к примеру:

5 = 2² + 1² + 0² + 0²;

6 = 2² + 1² + 1² + 0²;

7 = 2² + 1² + 1² + 1².

Теперь, стоило вам подумать о том, что для 8 потребуется еще одна 12, то есть пять квадратов, на помощь приходит 4:

8 = 2² + 2² + 0² + 0².

Эксперименты с более крупными числами позволяют с серьезным основанием предположить, что ответ должен быть «да», однако эта задача оставалась нерешенной более 1500 лет. Она получила известность как задача Баше по имени Клода Баше де Мезириака, опубликовавшего французский перевод «Арифметики» в 1621 г. Доказательство нашел Жозеф-Луи Лагранж в 1770 г. Не так давно были найдены более простые доказательства, основанные на абстрактной алгебре.