Иэн Стюарт - Математические головоломки профессора Стюарта

Могут ли существовать аналогичные теоремы для «карт» в пространстве, а не на плоскости? Области в пространстве будут представлять собой что-то вроде заполненных пузырей. Немного подумав, несложно догадаться, что для раскрашивания такой карты может потребоваться сколько угодно красок. Представьте, к примеру, что вы хотите нарисовать карту, для которой нужно шесть красок. Для начала возьмите шесть отдельных шаров. Пусть шар 1 выпустит пять тонких щупалец и коснется ими шаров 2, 3, 4, 5 и 6. Затем пусть шар 2 выпустит пять щупалец и коснется шаров 3, 4, 5 и 6. Затем перейдите к шару 3 и т. д. Получится, что каждая обросшая щупальцами область касается всех остальных областей и, следовательно, все шесть должны быть окрашены в разные цвета. Если проделать такую процедуру со 100 шарами, то потребуется 100 красок; если шаров будет миллион, красок тоже потребуется миллион. Короче говоря, числу необходимых красок нет предела.

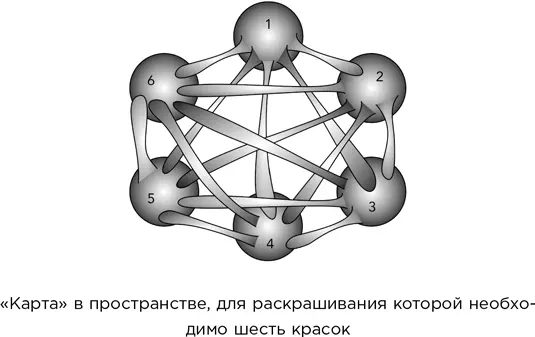
В 2013 г. Баскар Багчи и Басудеб Дата [33] Bhaskar Bagchi and Basudeb Datta. Higher dimensional analogues of the map coloring problem, American Mathematical Monthly 120 (October 2013) 733–736. поняли, что это не конец истории. Представьте себе «карты», сформированные из конечного числа кругов на плоскости, которые либо вообще не перекрывают друг друга, либо пересекаются в одной общей точке. Предположим, вы хотите раскрасить эти круги так, чтобы даже соприкасающиеся круги были окрашены в разные цвета. Сколько красок вам потребуется? Оказывается, ответ здесь такой же: не больше четырех.

На самом деле эта проблема по существу эквивалентна теореме о четырех красках. Эту теорему можно переформулировать в задачу раскрашивания узлов сети на плоскости с непересекающимися ребрами, так что если два узла этой сети соединены ребром, то эти узлы должны быть окрашены в разные цвета. Для этого достаточно просто создать по узлу для каждой области карты и соединить ребрами попарно те из них, области которых имеют общую границу. Можно доказать, что любая сеть на плоскости может быть собрана из подходящего набора кругов путем соединения центров тех кругов, которые касаются друг друга. К примеру, вот набор кругов, для окрашивания которых необходимы четыре цвета, связанная с ними сеть и карта с топологически эквивалентным искажением этой сети, для раскрашивания которой также требуется четыре краски.

Формулировку с кругами мы можем естественным образом распространить на три измерения, если используем шары вместо кругов. Опять же, эти шары либо вообще не перекрываются, либо касаются друг друга в общей точке. Предположим, вы хотите раскрасить шары так, чтобы те, которые касаются друг друга, были окрашены в разные цвета. Сколько красок вам понадобится? Багчи и Дата объяснили, почему это число не может быть меньше 5 и больше 13. Его точное значение до сих пор остается математической загадкой. Но вы, возможно, сумеете доказать, что нужно по крайней мере пять красок. Из их результата следует, что некоторые трехмерные карты не эквивалентны картам, построенным на базе шаров.

Ответ см. в главе «Загадки разгаданные».

Чтобы понять эту историю, вы должны быть немного знакомы с интегральным исчислением. Если ∫ – знак интеграла, то экспоненциальная функция e x – сама себе интеграл:

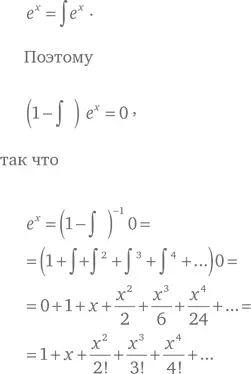
Эта формула кажется какой-то чепухой; даже первая строка должна была бы выглядеть как e x = ∫ e xdx, а 1 + y + y ² + y ³ + y 4+… = (1 – y)–1.

На следующем шаге в формуле для суммы бесконечной геометрической прогрессии переменная y заменяется на знак интеграла. Эта формула справедлива, если y – число, меньшее 1. Но ∫ – это даже не число, просто символ. Какой абсурд!

Несмотря на это, конечный результат – корректный степенн о й ряд для ex .

Это не совпадение. При правильных определениях (к примеру, ∫ – это оператор, превращающий функцию в ее интеграл, а формула для «суммы геометрической прогрессии» работает для операторов при подходящих технических условиях) все может выглядеть совершенно логичным. Но смотрится все равно странно.

Пал Эрдёш был весьма эксцентричным, блестящим венгерским математиком. Он никогда не имел дома, он никогда не занимал никакого ученого поста, предпочитая путешествовать по миру с небольшим чемоданом и ночевать в домах понимающих коллег. Он опубликовал 1525 математических статей и сотрудничал с 511 математиками – число, к которому никто другой в мире не смог даже приблизиться. Он предпочитал изобретательность глубоким систематическим занятиям теорией и с особенным удовольствием разгадывал загадки, которые выглядели очень просто, но на самом деле оказывались совсем не простыми. Его основные достижения относятся к области комбинаторики, но он мог бы приложить свою руку и ко многим другим областям математики. Он нашел новое доказательство постулата Бертрана (между n и 2 n всегда найдется хотя бы одно простое число), гораздо более простое, чем оригинальное аналитическое доказательство Пафнутия Чебышёва. Вершиной карьеры Эрдёша стало доказательство теоремы о числе простых (число простых чисел, меньших x , приблизительно равно x /ln x ), которая не поддавалась комплексному анализу, считавшемуся до того момента единственным способом доказательства.

Эрдёш любил предлагать денежные призы за решение задач, которые придумал, но не смог сам решить. Он мог предложить $25 за решение чего-то, что, как он подозревал, решается относительно просто, и несколько тысяч долларов за что-то, что он считал по-настоящему сложным. Типичный пример его математики – задача Эрдёша о расходимости, оцененная им в $500. Она была поставлена в 1932 г. и решена в начале 2014 г. Замечательный пример того, как сегодняшняя математика подходит к разрешению давних загадок.

Задача начинается с бесконечной последовательности чисел, равных или +1, или –1. Это может быть регулярная последовательность, к примеру

+1–1 +1–1 +1–1 +1–1 +1–1…,

или нерегулярная («случайная)

+1–1 –1–1 +1–1 +1 +1–1 +1…,

которую я получил путем бросания монетки. Она не обязана содержать равную долю плюсов и минусов. Подойдет любая последовательность.

Один из способов убедиться в том, что первая из этих последовательностей регулярна, – это взглянуть на каждый второй ее член: