Павел Полуэктов - Озадачник: 133 вопроса на знание логики, математики и физики
- Название:Озадачник: 133 вопроса на знание логики, математики и физики
- Автор:
- Жанр:
- Издательство:Литагент Альпина
- Год:2017
- Город:Москва
- ISBN:978-5-9614-4496-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Павел Полуэктов - Озадачник: 133 вопроса на знание логики, математики и физики краткое содержание
Озадачник: 133 вопроса на знание логики, математики и физики - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
57. Такие шахматы
[5]
У вас есть шахматная доска и 32 костяшки домино, причем размер костяшки – аккурат две клетки доски. Таким образом, вы без труда и большим числом способов сможете закрыть шахматную доску фишками домино. Срезаем по одной клетке в углах доски на концах одной из диагоналей – удастся ли 31 костяшкой закрыть все клетки такой доски?
1. Нет, это невозможно.
2. Да, одним-единственным способом.
3. Да, и способов сделать это – множество.
Ответ поражает – интуитивно-то нам кажется, что можно закрыть обрезанную доску 31 костяшкой, – но еще больше поражает красота и простота доказательства, почему этого сделать нельзя. Обратим внимание, что когда мы закрываем целую, неиспорченную доску, то каждая костяшка покрывает две клетки разного цвета – и черную, и белую, сделать так, чтобы клетки были одноцветные (две белые или две черные), не получится никоим образом. Теперь отметим тот факт, что клетки на концах любой диагонали доски 8 × 8 – одного цвета (для определенности будем считать, что белые), таким образом, после срезания двух клеток у нас на доске будут 62 белые и 64 черные клетки, или, иначе, у двух черных клеток не будет пары – отсюда с необходимостью следует, что покрыть такую доску 31 костяшкой не представляется возможным. Разве что одну из костяшек мы тоже решим порезать.
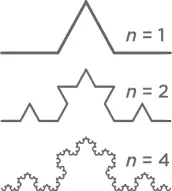
58. Какой длины?
Берем отрезок длины 1, выламываем из него посередине треть и заменяем ее на два отрезка, представляющие собой две стороны равностороннего треугольника, третьей стороной которого служит выброшенный нами отрезок. Затем с каждым звеном полученной ломаной проделываем то же самое, потом с новой ломаной, и так далее до бесконечности. Какой будет длина полученной в итоге линии?
1. 4/3.
2. Сумма бесконечного сходящегося ряда 1 + 1/3 + 1/3² +… = 3/2.
3. И не сосчитаешь!
Фигура, которая получается в итоге, – это кривая (еще говорят «снежинка») Коха (по имени автора, шведского математика Хельге фон Коха), один из самых известных фракталов – видимо, потому, что его проще всего рисовать. А еще несложно посчитать его длину на каждом этапе «сборки»: когда мы ломаем отрезок первый раз, мы заменяем среднюю часть (длины 1/3) на два отрезка, каждый такой же длины (треугольник по условию равносторонний). Сложим длины всех отрезков (1/3 + 1/3 + 1/3 + 1/3), получим 4/3. А какой будет длина ломаной на втором шаге? Очевидно, длина каждого маленького отрезка (1/3) увеличится, как видим из предыдущего рассуждения, в 4/3 раз, всего таких отрезков четыре, значит, суммарная длина всей ломаной будет уже (4/3)². И с каждым шагом эта степень будет увеличиваться, длина ломаной растет, причем экспоненциально, т. е. с каждым шагом все быстрее! Так, уже на четвертом шаге она будет превышать первоначальную втрое, на десятом – в 18 раз, на сотом – в 3 трлн раз! Фракталы на плоскости – удивительные фигуры, не имеющие ни длины (она, как видим, бесконечна), ни площади (она-то как раз равна нулю). Любопытно, что в жизни фракталы, про которые большинство людей даже не знает, встречаются на каждом шагу: это и деревья, и облака, и, конечно, снежинки.
59. Что загадать?
Вам и сопернику предлагают загадать натуральное число. Если загаданные вами числа совпадут, то вы оба получаете призы, если же они разные, то не получаете ничего. Какое число следует загадать?
1. Один.
2. Десять.
3. Любое, вероятность выигрыша одинакова и ничтожно мала.
Чем больше диапазон чисел, тем меньше шансов, что загаданное вами число совпадет с числом соперника. Так, если это диапазон от 1 до 10, шансы на совпадение только 10 %, если от 1 до 100, то только 1 %. Поэтому вам нужно максимально сузить этот диапазон, и это возможно в случае, если в диапазон попадает только одно число – от одного до одного. Если соперник станет руководствоваться той же логикой, то загаданные числа совпадут, приз будет ваш.

60. За спичками
В коробке лежит 21 спичка. Вы ходите первым, в игре у вас один соперник, каждый в свой ход (ходят поочередно) может взять от одной до трех спичек. Тот игрок, который не может больше сделать ход (спичек не осталось), проиграл. Можете ли вы выиграть в этой игре?
1. Да, тот, кто ходит первым, всегда может обеспечить себе победу.
2. Нет, выигрывает тот, кто ходит вторым.
3. Исход игры не предопределен, победит сильнейший.
Первый игрок гарантированно выигрывает, если берет столько спичек, чтобы остаток всегда был кратен 4. Для этого на первом ходу ему нужно взять одну спичку (остаток 20), затем взять столько, чтобы остаток равнялся 16 (если соперник взял одну – взять три; взял две – взять две; взял три – взять одну), затем, действуя аналогичным образом, взять столько, чтобы остаток равнялся 12, 8, 4, – когда остается четыре спички, сколько бы ни взял соперник, одну, две или три, вы забираете то, что осталось, тем самым обеспечив себе победу.
61. Путь самурая
Два самурая вышли одновременно – один направился из Токио в Киото, другой в обратном направлении, из Киото в Токио. Они встретились в 12:00, поклонились друг другу, как того требует кодекс самураев, и пошли дальше. Первый пришел в Токио в 16:00, второй в Киото в 21:00. В котором часу они начали свой путь? (Предполагаем, что дорога между Токио и Киото одна, а шли они все время с постоянной скоростью.)
1. В 4:00.
2. В 6:00.
3. В 8:00.
На первый взгляд, у нас слишком много неизвестных и слишком мало уравнений. Нам неизвестны: скорость первого самурая v 1, скорость второго v 2, расстояние от Токио до Киото L , а еще то, что требуется установить, – время, когда они отправились в путь t . А какие нам известны соотношения, связывающие их? L = v 1 × (16 – t ) = v 2× (21 – t ). И еще мы знаем, что в момент, когда они встретились (12:00), общее пройденное ими расстояние также равнялось L: L = ( v 1+ v 2) × (12 – t ). Как видим, L из этих соотношений мы легко можем исключить, и тогда у нас останется только два уравнения с тремя неизвестными v 1, v 2, t . То, что неизвестных больше, чем уравнений, показывает, что все их определить мы не сможем, найти скорости самураев не представляется возможным, но это и не требуется, ищем время t . Избавляемся от скоростей, переходя к их отношению v 1/ v 2и замечая, что из наших уравнений вытекает: это отношение равно (21 – t ) ∕ (16 – t ). В конечном итоге у нас получается квадратное уравнение t ² – 24 t + 108 = 0, которое элементарно решается и дает два корня t = 12 ± 6 = 6; 18. Очевидно, нам подходит только первое решение в силу простого соображения: они не могли стартовать позже , чем финишировал первый самурай (а это случилось, напомним, в 16:00).
Читать дальшеИнтервал:
Закладка:










