Павел Полуэктов - Озадачник: 133 вопроса на знание логики, математики и физики

– Ага, а зато у вас, – спорит самаркандец, – килограмм фиников на 60 сумов дороже, чем килограмм арбузов на рынке Самарканда!

Где же в действительности ниже цены, если на каждом рынке финики стоят вдвое дороже арбузов?

1. Цены в обоих городах одинаковы.

2. В Бухаре дешевле.

3. В Самарканде дешевле.

Простая арифметическая задачка, но ответ на нее совсем неочевиден, чтобы суметь ответить с ходу, не решая. Итак, пусть x – цена арбузов в Бухаре, y – в Самарканде (финики в Бухаре и Самарканде стоят 2 x и 2 y соответственно). Тогда у нас два уравнения: x + 30 = 2 y , 2 x – 60 = y , решая их, получаем x = 50, y = 40, в Самарканде, выходит, все на 20 % дешевле, чем в Бухаре.

Класс в полном составе отправляется на пейнтбол. Среди учеников особо выделяется Боря, которого все зовут Толстым Бо, он и правда не по годам широк.

– Бо, а ты же превосходная мишень! Вот в кого удобнее всего будет целиться, ты уж не обижайся, старик!

На полигоне всем раздали оружие и по четыре заряда к нему. После игры ребята, полностью расстреляв боекомплекты, подсчитывают «раны», и вот что выясняется: у трети класса (не считая Бо) по одному ранению, у другой трети – по два, и еще у трети – по три. Ну а на бедном Бо насчитали… 46 попаданий!

Вопрос: сколько учеников в классе Толстого Бо?

1. 17.

2. 22.

3. 25.

x – искомое число учеников, посчитаем их «раны»: 1 × ( x – 1)/3 + 2 × ( x – 1)/3 + 3 × ( x – 1)/3 + 46, и созданы они были теми зарядами, что ребята друг в друга выпустили, общим числом 4 x . Таким образом, уравнение на x будет: 2 x – 2 + 46 = 4 x, x = 22.

Числа A, B, C и D связаны соотношениями: A – 3 = B + 8 = С – 5 = D . Какое из чисел является наименьшим?

1. B .

2. C .

3. D .

Сравним все числа с D: A больше D на 3, C больше D на 5, а B меньше D на 8. Значит, B меньше и D , и A , и C , т. е. меньше всех.

В коробке лежат 5 белых, 8 красных и 13 черных шаров. Какое минимальное число шаров нужно вытащить (вслепую, их цвет в момент выбора нам неизвестен), чтобы там было по меньшей мере два шара одного цвета?

1. Четыре.

2. Шесть.

3. Девять.

Если нам очень повезет, сразу два первых шара будут одного цвета (скорее всего, черного). В самом же худшем случае три первых шара будут разного цвета: белый, красный, черный. Но четвертый шар будет либо белый, либо красный, либо черный, иного не дано. Значит, вытащив четыре шара, мы гарантированно имеем два одного цвета.

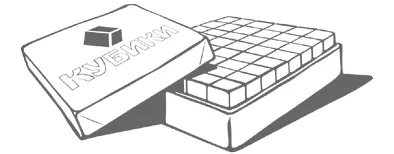
Размеры коробки для кубиков – 40 × 30 × 10 см. Сколько кубиков в коробке?

1. 24.

2. 48.

3. 96.

Очередная диофантова задача (см. задачу № 47). Мы предполагаем, что кубики плотно заполняют коробку, т. е. занимают весь ее объем. Что ж, посчитаем размер кубика для варианта 1. Объем кубика будет равен 12 000 куб. см (объем коробки) разделить на 24 (количество кубиков), что дает 500 куб. см. Длина ребра кубика суть корень кубический из этого числа, не выражается в рациональных числах и приближенно равна 7,93 см. Очевидно, кубики с таким ребром плотно в нашу коробку не вместить, ведь ни 20, ни 30, ни 40 на 7,93 нацело не делятся. Аналогично с вариантом 2 (48 кубиков), объем кубика получается 250 куб. см, длина ребра – 6,3 см. А вот когда кубиков 96, то объем каждого – 125 куб. см, а значит, длина ребра 5 см, и такие кубики спокойно уместятся в нашей коробке, по восемь кубиков в длину, шесть в ширину и два в высоту.

Ситуация с пропускной способностью метро – тупиковая: интервал между поездами уменьшить нельзя (тогда они начнут догонять друг друга в тоннелях), длина состава ограничена длиной платформы – все, потолок, увеличить пассажиропоток решительно невозможно! Но тут в мэрии предлагают неожиданное решение: сцеплять поезда друг с другом ( k = 2, 3, 4 состава вместе), чтобы такой суперпоезд останавливался на каждой платформе k раз, для посадки и высадки пассажиров из каждой из своих частей. Мол, время простоя на станции несколько увеличится, зато пассажиров такой поезд в k раз больше сможет взять за один рейс! Интересное решение, но будет ли от него толк?

1. Разумеется, да, отличное решение!

2. Смотря для кого: для метрополитена в целом да, для пассажиров – нет.

3. Вот же глупость какая!

У нас есть четыре параметра: вместимость состава (обозначим Q) и три времени – среднее время в пути между двумя станциями ( t тоннель), время на посадку-высадку пассажиров ( t посадка) и время сдвига поезда на платформе ( t сдвиг) – то, за которое суперпоезд переместится на длину одного состава обычного поезда. При этом пассажиропоток (P) определяется как P = kQ / t , где t – полное время, t = t тоннель+ kt посадка + ( k – 1) t сдвиг(где k раз совершили посадку-высадку и k – 1 раз сдвинули состав). Перепишем в более компактной форме: t = t 0+ ( k – 1) × τ, t 0= t тоннель+ t посадка(стандартное полное время для обычного поезда), τ = t посадка+ t сдвиг – «добавка» за счет удлинения. Что можно сказать о пассажиропотоке? Если k очень большое ( k >> 1), то, как нетрудно заметить, P → P 0 t 0/τ, где P 0= Q / t 0 – пассажиропоток обычного поезда. Если t 0< τ, то задача теряет смысл – суперпоезд будет возить меньше пассажиров, чем обычный. Но возьмем реалистичные значения, скажем, t 0= 3 мин, τ = 1 мин. Тогда пассажиропоток мы можем, в пределе, утроить (если возьмем очень большое число составов k ). Впрочем, уже при k = 4 пассажиропоток возрастет вдвое! Правда, и время в пути возрастет также вдвое (за счет долгого стояния на станциях). Ехать придется долго – зато свободно.