Саймон Сингх - Симпсоны и их математические секреты

Сценаристы стимулировали расцвет интеллекта Гомера и в эпизоде «Они спасли мозг Лизы», о котором шла речь в главе 7. После того как Стивен Хокинг увозит Лизу от разъяренной толпы, действие перемещается в бар Мо, где беседуют профессор Хокинг и Гомер. На ученого производят впечатление идеи Гомера по поводу космологии: «Гомер, твоя теория пончикообразной Вселенной заинтриговала меня. Я ее у тебя украду».

Хотя это звучит нелепо, но специалисты по космологии с математическим складом ума утверждают, что Вселенная действительно могла бы иметь структуру пончика. Для того чтобы объяснить вероятность такой геометрии, давайте упростим Вселенную, представив себе, что все космическое пространство стало плоским в результате перехода из трех– в двухмерное измерение, так что все сущее расположено на листе. Здравый смысл подсказывает, что этот вселенский лист должен быть плоским и простираться до бесконечности во всех направлениях. Однако космология редко согласуется со здравым смыслом. Эйнштейн учил нас, что пространство может искривляться, что в результате приводит к самым разным сценариям развития событий. Например, представьте себе, что лист Вселенной не бесконечен, а имеет четыре края и напоминает скорее большой прямоугольный лист резины. Далее вообразите, что вы соединяете две его длинные стороны так, чтобы образовать цилиндр, а затем соединяете два конца этого цилиндра, чтобы весь лист превратился в пустотелый пончик. Это и есть та модель Вселенной, которую обсуждали Хокинг и Гомер.

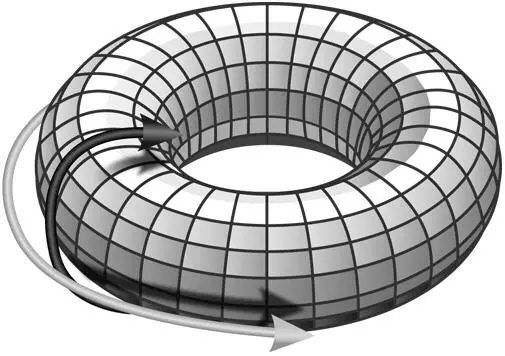
Если бы вы жили на поверхности этой пончикообразной Вселенной, то могли бы перемещаться по серой стрелке и в конце концов вернуться в исходное положение. Вы могли бы также отправиться по черной стрелке и снова оказались бы там, откуда начали движение. Пончикообразная Вселенная ведет себя как космическое пространство в популярной видеоигре Asteroids компании Atari. Если корабль игрока летит на восток, то он исчезает с экрана с правой стороны и снова появляется с левой. Точно так же, если корабль отправляется на север, он доходит до верхнего края экрана, после чего появляется в нижней его части, опять вернувшись в отправную точку.

Безусловно, мы проанализировали эту теорию только в контексте двух измерений, но согласно законам физики трехмерную Вселенную тоже можно свернуть в цилиндр, образуя своего рода пончик. Человеку, не имеющему отношения к математике, почти невозможно представить себе такие манипуляции с трехмерным пространством, но Хокинг и Гомер понимают, что пончик – это идеальная, вполне жизнеспособная, реальная форма для Вселенной. Британский ученый Джон Бердон Сандерсон Холдейн (1892–1964) однажды сказал: «Подозреваю, что Вселенная не только причудливее, чем мы себе представляем, но и причудливее, чем мы можем представить».

В других эпизодах сценаристы создают то или иное триггерное (переключающее из одного положения в другое) событие, которое стимулирует мозг Гомера, что, в свою очередь, позволяет ему добиваться успехов в математике. В эпизоде «ГОМР» (HOMR, сезон 12, эпизод 9; 2001 год) Гомер удаляет из своего мозга карандаш и вдруг осознает, что может использовать высшую математику, чтобы доказать, что Бога не существует. Он показывает доказательство своему богобоязненному соседу Неду Фландерсу, который сначала с подозрением относится к заявлению Гомера, что Бог исчезает под натиском логики. Но затем Фландерс анализирует доказательство и бормочет: «Ну-ка посмотрим… Может быть, он ошибся… Нет. Все верно. Эту бумагу никто не должен видеть». Фландерсу не удается найти ни одной ошибки в доказательстве Гомера, поэтому он решает сжечь лист, на котором оно написано.

Эта сцена отдает дань уважения одному из самых известных случаев в истории математики, когда величайший математик XVIII столетия Леонард Эйлер сделал вид, что доказал нечто противоположное выводу Гомера, а именно – что Бог существует. Инцидент произошел в тот период, когда Эйлер находился при дворе Екатерины Великой в Санкт-Петербурге. Екатерину и ее придворных все больше беспокоило влияние гостившего у них французского философа Дени Дидро, который был убежденным атеистом и, по слухам, приходил в ужас от математики. Эйлера попросили составить фальшивое уравнение, которое бы доказывало существование Бога и положило конец ереси Дидро. Когда Эйлер обнародовал это уравнение, Дидро потерял дар речи. После этого он стал объектом насмешек всего Петербурга и вскоре попросил разрешения вернуться в Париж.

Мозг Гомера получает еще один временный стимул в эпизоде «$прингфилд (или как я перестал бояться и полюбил легальные азартные игры)» ($pringfield (Or, How I Learned to Stop Worrying and Love Legalized Gambling), сезон 5, эпизод 10; 1993 год). В самом начале эпизода Генри Киссинджер (в какой-то мере необъяснимо) совершает прогулку по территории места работы Гомера, Спрингфилдской атомной электростанции. К сожалению, бывший госсекретарь США роняет свои фирменные очки в унитаз, когда заходит в один из туалетов электростанции. Будучи слишком робким, чтобы вытащить их оттуда, и слишком смущенным, чтобы попросить кого-то о помощи, Киссинджер бормочет себе под нос: «Никто не должен знать, что я упустил их в унитаз. Только не я, человек, написавший проект Парижского мирного соглашения».

Вскоре в ту же туалетную кабинку заходит Гомер и обнаруживает в унитазе очки. Разумеется, он не может не вытащить их оттуда, после чего очки как будто наделяют его силой разума Киссинджера. Все еще находясь в туалете, Гомер начинает как заведенный повторять математическую формулу:

Сумма квадратных корней [38]любых двух сторон равнобедренного треугольника равна квадратному корню оставшейся стороны.

На первый взгляд может показаться, что это простое проговаривание теоремы Пифагора, но в действительности это не так по нескольким причинам. Настоящая теорема Пифагора гласит:

Квадрат гипотенузы прямоугольного треугольника равен сумме квадратов смежных сторон.

Самое очевидное различие состоит в том, что утверждение Гомера касается равнобедренного треугольника, тогда как теорема Пифагора описывает прямоугольный треугольник. Возможно, вы еще со школы помните, что равнобедренный треугольник имеет две стороны одинаковой длины, тогда как прямоугольный треугольник может иметь стороны любой длины, если один его угол прямой.

В утверждении Гомера есть еще две проблемы. Во-первых, он говорит о «квадратных корнях» сторон треугольника, тогда как в теореме Пифагора идет речь о квадратах сторон. Во-вторых, теорема Пифагора устанавливает зависимость между гипотенузой (самой длинной стороной прямоугольного треугольника) и двумя катетами, тогда как Гомер ставит «любые две стороны» равнобедренного треугольника в зависимость от «оставшейся стороны». В качестве «любых двух сторон» могут выступать либо две равные стороны, либо одна из равных сторон и неравная сторона.