Саймон Сингх - Симпсоны и их математические секреты

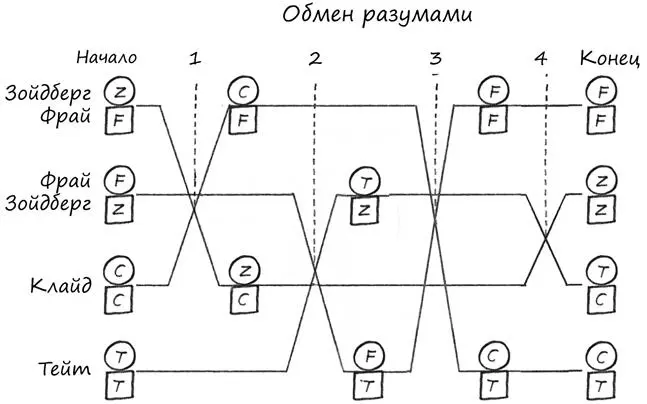
Милейший Клайд и Баблгам Тейт все еще перепутаны, поэтому очевидно, что на следующем этапе необходимо вернуть их разумы в свои тела, выполнив всего один обмен – и это возможно, потому что они еще не менялись разумами друг с другом. Однако пока это преждевременно. Маскетбольные гении включены в общую совокупность персонажей, обменявшихся разумами, с целью распутать два множества, поэтому их миссия еще не закончена. Следовательно, они должны оставаться с перепутанными телами и разумами, пока не решат проблему со вторым множеством.

Ниже представлена диаграмма Сили, на которой показано девять обменов разумами в процессе упорядочивания второго множества. Нет надобности анализировать ее пошагово, но общая закономерность показывает, как включение Милейшего Клайда и Баблгама Тейта создает место для маневра, необходимое для разрешения ситуации. Оба персонажа вовлечены в каждый обмен разумами, что объясняет высокую плотность диаграммы в нижней четверти. Милейший Клайд и Баблгам Тейт выступают в качестве сосудов для тех разумов, которые ищут свой дом. Получив тот или иной разум, они тут же совершают такой обмен, чтобы этот разум оказался в конечном счете в подходящем теле. Какой бы разум Клайд и Тейт ни получили, они сразу же передают его в соответствующее тело во время следующего обмена и т. д.

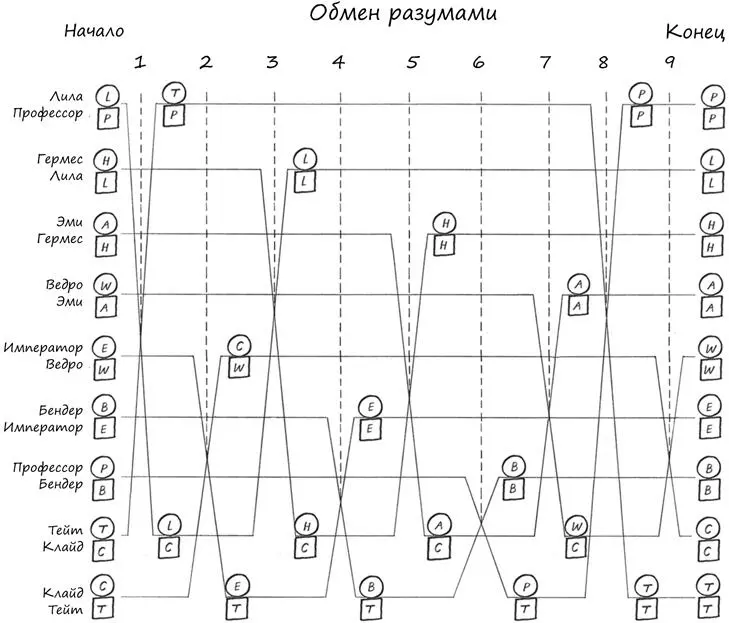
Хотя Килер проделал отличную работу, решив задачу обмена разумами и доказав теорему Футурамы, тем не менее важно отметить, что он либо упустил один момент, либо сознательно проигнорировал его, для того чтобы сделать финал эпизода «Узник Бендера» более эффектным. Речь идет о еще одном, более коротком пути решения этой задачи. Если вы помните, для того чтобы распутать любую ситуацию, необходимо ввести двух новых персонажей. Однако в сценарии, который мы анализируем, одно из упорядочиваемых множеств состоит всего из двух человек (разум Фрая в теле Зойдберга и разум Зойдберга в теле Фрая). Следовательно, они могли бы выступить в качестве двух новых персонажей по отношению к более крупному множеству. Это возможно, поскольку Фрай и Зойдберг еще не обменивались разумами ни с одним персонажем, входящим в него.

Двухэтапный процесс возвращения разумов в свои тела, который имеет место в эпизоде, потребовал сначала четырех обменов, а затем еще девяти, что в сумме дает тринадцать обменов. Напротив, если использовать более короткий путь, то все разумы можно было бы вернуть в свои тела посредством всего девяти обменов.

Использование существующего множества для получения двух дополнительных персонажей, необходимых для распутывания другого множества, впервые проанализировал Джеймс Крайм, математик из Кембриджа (Англия). Поэтому некоторые называют этот метод следствием Крайма , которое представляет собой математическое утверждение, вытекающее из теоремы Футурамы.

Теорема Килера вдохновила Рона Эванса, Лихуа Хуана и Туан Нгуен на написание научной работы по теме обмена разумами под названием Keeler’s Theorem and Products of Distinct Transpositions («Теорема Килера и результаты различных транспозиций»), которая была опубликована в журнале American Mathematical Monthly. В этой работе анализируются пути наиболее эффективного разрешения любой ситуации с обменом разумами.

Сам Килер решил не публиковать результаты исследований по задаче с обменом разумами. Он скромно называет свою теорему обычной математической задачей и не очень охотно поддерживает разговоры относительно ее доказательства. По его словам, самое подробное описание ее доказательства было в поддельном сценарии, который он раздал коллегам: «Когда сценарист сдает свой вариант сценария, первый этап процесса редактирования состоит в том, что все остальные сценаристы получают копии и около получаса читают сценарий. В качестве розыгрыша на трех страницах в самом начале сценария я описал сцену, в которой Милейший Клайд во всех подробностях объясняет свою теорему профессору. Некоторые сценаристы с трудом одолели все это описание, ничего не заподозрив, прежде чем поняли, что настоящий сценарий начинается на четвертой странице».

Шутливый сценарий, который Килер использовал для розыгрыша коллег, подчеркивает тот факт, что в основе настоящего сценария к эпизоду «Узник Бендера» лежит поистине интересная и новаторская математическая теорема. Во многом этот эпизод – вершина всех математических ссылок, присутствующих как в «Симпсонах», так и в «Футураме». Майк Рейсс и Эл Джин начали с включения математических шуток в режиме стоп-кадра в эпизоды первого сезона «Симпсонов», а два десятилетия спустя Кен Килер создал совершенно новую теорему, чтобы помочь экипажу «Межпланетного экспресса». На самом деле Килер может претендовать на звание первого сценариста в истории телевидения, который вывел новую математическую теорему исключительно для целей комедийного сериала.

Шутка 1

Вопрос:Что пурпурное и коммутирует?

Ответ:Абелев виноград.

1 балл

Шутка 2

Вопрос:Что лиловое и коммутирует?

Ответ:Абелев полувиноград.

1 балл

Шутка 3

Вопрос:Что питательное и коммутирует?

Ответ:Абелев суп.

1 балл

Шутка 4

Вопрос:Что пурпурное, коммутирует, и ему поклоняется ограниченное количество людей?

Ответ:Конечно, почитаемый абелев виноград.

1 балл

Шутка 5

Вопрос:Что пурпурное, опасное и коммутирует?

Ответ:Абелев виноград с автоматом.

1 балл

Шутка 6

Вопрос:Что большое, серое и доказывает неисчислимость десятичных чисел?

Ответ:Диагональный слон Кантора.

2 балла

Шутка 7

Вопрос:Какая самая длинная в мире песня?

Ответ:«ℵ 0бутылок пива на стене».

2 балла

Шутка 8

Вопрос:Что означает «Б.» в имени «Бенуа Б. Мандельброт»?

Ответ:Бенуа Б. Мандельброт.

4 балла

Шутка 9

Вопрос:Как называется молодой собственный баран? (Англ. eigensheep («собственный баран») созвучно с eigen shift – «сдвиг спектра собственных чисел».)

Ответ:Понятное дело, ягненок!

1 балл

Шутка 10

Однажды управляющего королевской фабрики по производству доспехов попросили прислать образец, для того чтобы попробовать получить очень большой заказ на выпуск туник и рейтуз.