Саймон Сингх - Симпсоны и их математические секреты

Сценаристы включили в эпизод сбой в работе мозгообменника, чтобы сделать сюжет интереснее. Однако кому-то надо было найти способ решить эту проблему и обеспечить счастливый конец истории. Ответственность легла на Кена Килера, ведущего сценариста данного эпизода. Килер понимал, что единственный выход из создавшегося тупика – включить в сценарий новых персонажей, способных обеспечить косвенные пути, с помощью которых профессор и остальные герои могли бы вернуться в свои тела. Но вместо того чтобы заняться самим сценарием «Узника Бенды», Килер сфокусировался на более общей задаче: сколько новых людей необходимо включить в группу любого размера, чтобы распутать неразбериху, возникшую в результате обмена разумами?

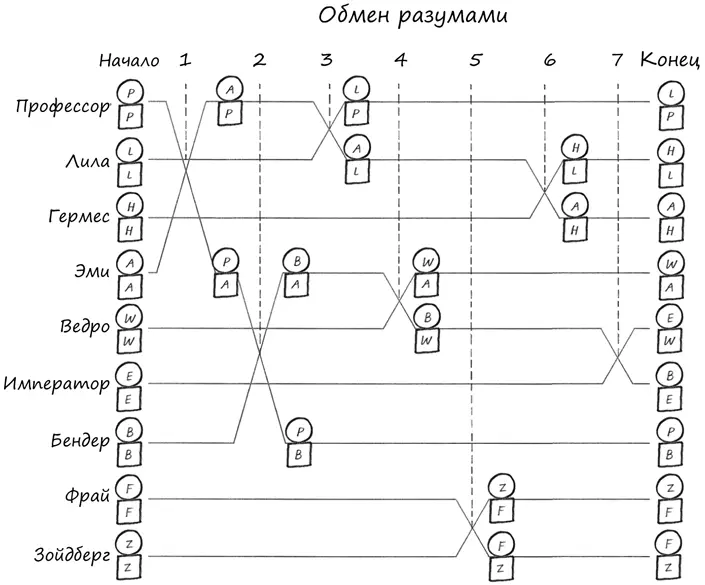
Эта диаграмма Сили демонстрирует процесс обмена разумами. Кружочками отмечены разумы, квадратиками – тела, а расположенные внутри них буквы соответствуют различным персонажам. Сначала девять пар «разум-тело» совпадают, поскольку каждый разум изначально находится в своем теле. Затем разумы переходят в другие тела после очередного обмена. Например, после первого обмена тело профессора получает разум Эми, и наоборот. Тела всегда остаются на одной горизонтальной линии, тогда как разумы перемещаются в случае обмена либо вверх, либо вниз.

Когда Килер начал исследовать проблему, у него не было никаких догадок по поводу ее решения. Будет ли количество новых людей зависеть от численности членов группы? Если да, то, может, количество новых людей будет прямо пропорционально численности группы или оно находится в экспоненциальной зависимости от ее размера? Или, возможно, существует некое волшебное количество новых персонажей, которые могли бы решить проблему в группе любого размера?

Эту фотографию сделал Патрик Веррон 9 декабря 2009 года, во время вычитки сценария эпизода «Узник Бенды». Кен Килер делает набросок доказательства теоремы Футурамы, стоя на диване в офисе «Футурамы».

Из личного архива Патрика Веррона

Поиск ответа на эти вопросы оказался непростым даже для человека со степенью доктора наук в области прикладной математики. Это напомнило Килеру о нескольких еще более трудных задачах, с которыми он сталкивался в университете. После продолжительного мозгового штурма Килер сформулировал неопровержимое доказательство, которое обеспечивало бесспорный результат. Решение оказалось на удивление изящным. Килер пришел к выводу, что включения всего двух персонажей будет достаточно, чтобы распутать любую неразбериху с обменом разумами, при условии, что оба человека будут задействованы правильно. Доказательство Килера, носящее несколько формальный характер, получило известность как теорема Футурамы, или теорема Килера .

В эпизоде «Узник Бенды» это доказательство представляют «Милейший» Клайд Диксон и Итан «Баблгам» Тейт, два баскетболиста с планеты Мир Глобтроттеров, которые известны также своими способностями к математике и другим точным наукам. На самом деле Баблгам Тейт – старший преподаватель физики в Глобтроттерском университете и профессор прикладной физики в Марсианском университете. Оба персонажа появляются в нескольких эпизодах «Футурамы» и постоянно демонстрируют свои математические таланты. Например, в полнометражном мультфильме «Большой куш Бендера» Баблгам Тейт дает Милейшему Клайду совет по поводу решения уравнения, описывающего путешествия во времени: «Милейший Клайд, используй вариации переменных и выполни разложение детерминанта Вронского» [60].

Когда эпизод «Узник Бендера» приближается к развязке, Милейший Клайд пишет доказательство на зеленой флуоресцентной доске, а затем заявляет: «В принципе не важно, насколько переставлены ваши разумы; они могут быть возвращены с помощью максимум двух дополнительных игроков».

Теорема Футурамы, записанная на доске Милейшим Клайдом в конце эпизода «Узник Бенды». Баблгам Тейт внимательно изучает детали доказательства, тогда как Бендер (в теле которого находится разум профессора Фарнсворта) восхищенно смотрит на доску. Расшифровку представленного на доске доказательства можно найти в Приложении 5.

FUTURAMA © 2002 Twentieth Century Fox Television. Все права защищены

Лучший способ понять доказательство, сформулированное в специальных терминах, – сфокусироваться на том, как оно может помочь героям эпизода «Узник Бендера» найти выход из трудного положения, в которое они попали. Фактически это доказательство описывает хорошо продуманную стратегию устранения путаницы, которая начинается с осознания того, что всех людей, обменявшихся разумами, можно отнести к однозначно определенным множествам; в случае «Узника Бенды» таких множеств два. Тщательный анализ диаграммы Сили позволяет сделать вывод, что в первое множество входят Фрай и Зойдберг. Это становится понятно по двум нижним строкам диаграммы, которые говорят о том, что разум Фрая находится в теле Зойдберга, а разум Зойдберга – в теле Фрая. Данную совокупность можно считать множеством, поскольку мы видим, что для каждого тела есть разум, и единственная проблема состоит в том, что эти тела и разумы перепутаны.

Во второе множество входят все остальные персонажи. Диаграмма Сили показывает, что разум профессора оказался в теле Бендера, разум Бендера – в теле Императора, разум Императора – в теле Ведра, разум Ведра – в теле Эми, разум Эми – в теле Гермеса, разум Гермеса – в теле Лилы, а разум Лилы – в теле профессора, что замыкает множество. Эта совокупность тоже считается множеством, поскольку для каждого тела есть разум, но тела и разумы перемешаны.

Определив множества, Килер включил в общую совокупность еще двоих человек, Баблгама Тейта и Милейшего Клайда, которые затем совершают обмен разумами в каждом из двух множеств. Для того чтобы увидеть процесс в действии, давайте начнем с меньшего множества и упорядочим его.

На представленной ниже диаграмме Сили показано, что именно происходит в эпизоде. Мы видим, что этап возврата разумов в свои тела начинается с обмена разумами между Милейшим Клайдом и Фраем (в теле которого находится разум Зойдберга); затем Баблгам Тейт обменивается разумом с Зойдбергом (в теле которого разум Фрая). После еще двух обменов разум Фрая возвращается в свое тело, а разум Зойдберга – в свое.