Яков Перельман - Живая математика. Математические рассказы и головоломки

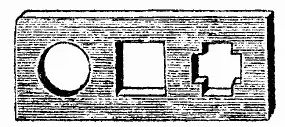
Рис. 103. Существует ли одна затычка к трем отверстиям такой формы?

Рис. 104. Можно ли для этих трех отверстий изготовить одну затычку?

Как вы думаете: пролезет пятак через эту дырку? Здесь нет подвоха - задача подлинно геометрическая.

В нашем городе есть достопримечательность - высокая башня, высоты которой вы, однако, не знаете. Имеется у вас и фотографический снимок башни на почтовой карточке. Как может этот снимок помочь вам узнать высоту башни?

Эта задача предназначается для тех, кто знает, в чем состоит геометрическое подобие. Требуется ответить на следующие два вопроса:

1) В фигуре чертежного треугольника (рис. 105)подобны ли наружный и внутренний треугольники?

2) В фигуре рамки (рис. 106)подобны ли наружный и внутренний четырехугольники?

Рис. 105. Подобны ли наружный и внутренний треугольники?

Рис. 106. Подобны ли наружный и внутренний четырехугольники?

Как далеко в солнечный день тянется в пространстве полная тень, отбрасываемая телеграфной проволокой, диаметр которой 4 мм?

Строительный кирпич весит 4 кг. Сколько весит игрушечный кирпичик из того же материала, все размеры которого в 4 раза меньше?

Во сколько примерно раз великан ростом 2 м тяжелее карлика ростом 1 м?

Продаются два арбуза неодинаковых размеров. Один на четвертую долю шире другого, а стоит он в 1 1/ 4раза дороже.

Какой из них выгоднее купить (рис. 107)?

Продаются две дыни одного сорта. Одна окружностью 60, другая - 50 см. Первая в полтора раза дороже второй.

Какую дыню выгоднее купить?

Мякоть вишни окружает косточку слоем такой же толщины, как и сама косточка. Будем считать, что и вишня, и косточка имеют форму шариков.

Можете ли вы сообразить в уме, во сколько раз объем сочной части вишни больше объема косточки?

Рис. 107

Башня Эйфеля в Париже, 300 м высоты, сделана целиком из железа, которого пошло на нее около 8 000 000 кг.

Я желаю заказать точную железную модель знаменитой башни, весящую всего только 1 кг. Какой она будет высоты? Выше стакана или ниже?

Имеются две медные кастрюли одинаковой формы и со стенками одной толщины. Первая в 8 раз вместительнее второй.

Во сколько раз она тяжелее?

Рис. 108. Башня Эйфеля в Париже

На морозе стоят взрослый человек и ребенок, оба одетые одинаково.

Кому из них холоднее?

Что тяжелее: стакан сахарного песку или такой же стакан колотого сахара?

64. На первый взгляд задача эта кажется не относящейся вовсе к геометрии. Но в том-то и состоит овладение этой наукой, чтобы уметь обнаруживать геометрическую основу задачи там, где она замаскирована посторонними подробностями. Наша задача по существу, безусловно, геометрическая; без знания геометрии ее не решить.

Итак, почему же передняя ось телеги стирается больше задней? Всем известно, что передние колеса меньше задних. На одном и том же расстоянии малый круг оборачивается большее число раз, чем круг покрупнее: у меньшего круга и окружность меньше - оттого она укладывается в данной длине большее число раз. Теперь понятно, что при всех поездках телеги передние ее колеса делают больше оборотов, нежели задние; а большее число оборотов, конечно, сильнее стирает ось.

65. Если вы полагаете, что в лупу угол наш окажется величиною в 1 1/ 4х 4 = 6°, то дали промах. Величина угла нисколько не увеличивается при рассматривании его в лупу.

Рис. 109. Передние колеса телеги меньше задних

Правда, дуга, измеряющая угол, несомненно, увеличивается, но во столько же раз увеличивается и радиус этой дуги, так что величина центрального угла остается без изменения. Рис. 109 поясняет сказанное. Невозможность увеличения углов лупой вытекает, между прочим, и прямо из того, что фигуры при рассматривании в лупу сохраняют геометрическое подобие самим себе. Если бы каждый угол многоугольника увеличивался в 4 раза, то мы видели бы в лупу квадраты с углами в 360° или треугольники, сумма углов которых равна 8 прямым!

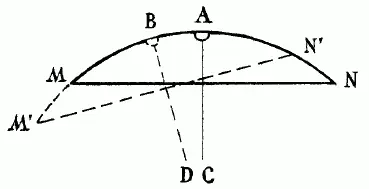
Рис. 110

66. Рассмотрите рис. 110, где MAN есть первоначальное положение дуги уровня, M’BN ’- новое ее положение, причем хорда JVPN' составляет с хордой MN угол в 1/ 2°. Пузырек, бывший раньше в точке А, теперь остался в той же точке, но середина дуги MN переместилась в В. Требуется вычислить длину дуги АВ, если радиус ее равен 1 м, а величина дуги в градусной мере 1/ 2° (это следует из равенства острых углов с перпендикулярными сторонами). Вычисление несложно. Длина полной окружности радиусом в 1 м (1000 мм) равна 2 х 3,14 х 1000 = 6280 мм. Так как в окружности 360°, или 720 полуградусов, то длина одного полуградуса определяется делением:

6280: 720 = 8,7 мм.

Пузырек отодвинется от метки (вернее, метка отодвинется от пузырька) примерно на 9 адм - почти на целый сантиметр. Легко видеть, что чем больше радиус кривизны трубки, тем уровень чувствительнее.

67. Задача вовсе не шуточная и вскрывает ошибочность обычного словоупотребления. У «шестигранного» карандаша не 6 граней, как, вероятно, полагает большинство. Всех граней у него, если он не очинен, 8: шесть боковых и еще две маленькие «торцовые» грани. Будь у него в действительности 6 граней, он имел бы совсем иную форму - бруска с четырех-угольным сечением. Привычка считать у призм только боковые грани, забывая об основаниях, очень распространена. Многие говорят: «трехгранная» призма, «четырехгранная» призма и т. д., между тем как призмы эти надо называть: треугольная, четырехугольная и т. д. - по форме основания. Трехгранной призмы, т. е. призмы о трех гранях, даже и не существует.