Яков Перельман - Живая математика. Математические рассказы и головоломки

Поэтому карандаш, о котором говорится в задаче, правильно называть не шестигранным, а шестиугольным.

68. Сделать надо так, как показано на рис. 111.Получаются 6 частей, которые для наглядности перенумерованы.

69. Спички следует расположить, как показано слева на рис. 112;площадь этой фигуры равна учетверенной площади «спичечного» квадрата.

Как в этом удостовериться?

Дополним мысленно нашу фигуру до треугольника. Получится прямоугольный треугольник, основание которого равно 3, а высота 4 спичкам [25] Читатели, знакомые с так называемой «пифагоровой теоремой», поймут, почему мы с уверенностью можем утверждать, что получающийся здесь треугольник – прямоугольный: З 2 + 4 2 = 5 2 . . Площадь его равна половине произведения основания на высоту:

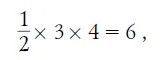
т. е. 6 квадратам со стороною в одну спичку. Но наша фигура имеет, очевидно, площадь, которая меньше площади треугольника на 2 «спичечных» квадрата и равна, следовательно, 4 таким квадратам.

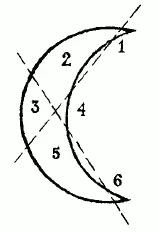
Рис. 111

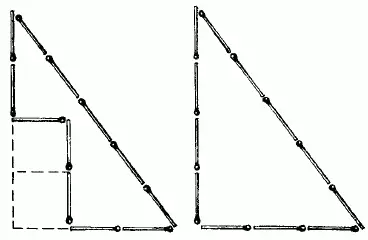
Рис. 112

Рис. 113

70. Можно доказать [26] Доказательство приведено в «Занимательной геометрии» того же автора. , что среди всех фигур с одинаковым обводом наибольшую площадь имеет круг. Из спичек, конечно, не сложить круга; однако можно составить из 8 спичек фигуру (рис. 113), всего более приближающуюся к кругу - это правильный восьмиугольник. Правильный восьмиугольник и есть фигура, удовлетворяющая требованию нашей задачи: она имеет наибольшую площадь. Эта задача приводит на память легендарную историю основателя Карфагена. Дидона, дочь финикийского царя, гласит предание, потеряв мужа, убитого ее братом, бежала в Африку и высадилась со многими финикийцами на северном ее берегу. Здесь Дидона купила у нумидийского царя столько земли, «сколько занимает воловья шкура». Когда сделка состоялась, Дидона разрезала воловью шкуру на тонкие ремешки и благодаря подобной уловке отхватила участок земли, достаточный для сооружения крепости. Так будто бы возникла крепость Карфаген, вокруг которой впоследствии вырос город.

Прикинем, какая примерно площадь могла быть захвачена хитростью Дидоны. Если поверхность воловьей шкуры была равна 4 кв. м, т. е. 4 000 000 кв. мм, а ширина ремней 1 мм, то общая длина вырезанных ремней достигала 4 000 000 мм, или 4 км. Ремнем такой длины можно охватить квадратный участок площадью в 1 кв. км. Но Дидона получила бы еще больше земли, если бы окружила ремнем круглый участок (около 1,3 кв. км).

71. Для решения задачи развернем боковую поверхность цилиндрической банки в плоскую фигуру: получим прямоугольник (рис. 114),высота которого 20 см, а основание равно окружности банки, т. е. 10 х 3 1/ 7 = 31 1/ 2см (без малого). Наметим на этом прямоугольнике положения мухи и медовой капли. Муха - в точке А, на расстоянии 17 см от основания; капля - в точке В, на той же высоте и на расстоянии полуокружности банки от А, т. е. в 15 3/ 4см. Чтобы найти теперь точку, в которой муха должна переползти край банки, поступим следующим образом. Из точки В (рис. 115)проведем прямую под прямым углом к верхней стороне прямоугольника и продолжим ее на равное расстояние: получим точку С. Эту точку соединим прямой линией с А. Точка D, как учит геометрия, и будет та, где муха должна переползти на другую сторону банки, а путь ADB окажется самым коротким.

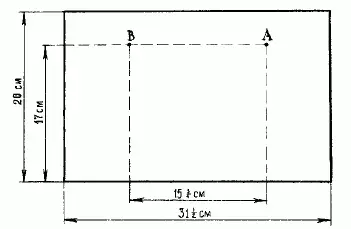
Рис. 114

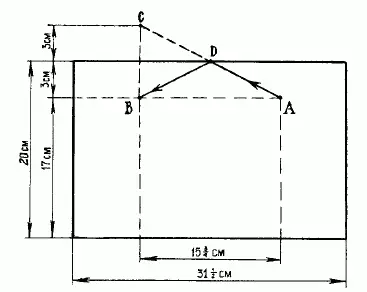
Рис. 115

Найдя кратчайший путь на развернутом прямоугольнике, свернем его снова в цилиндр и узнаем, как должна бежать муха, чтобы скорее добраться до капли меда (рис. 116).Избирают ли мухи в подобных случаях такой путь - мне неизвестно. Возможно, что, руководствуясь обонянием, муха действительно пробегает по кратчайшему пути, но маловероятно: обоняние для этого - недостаточно четкое чувство.

Рис. 116. Кратчайший путь мухи

72. Нужная в данном случае затычка существует. Она имеет форму, показанную на рис. 117.Легко видеть, что одна такая затычка действительно может закрыть и квадратное, и треугольное, и круглое отверстие.

73. Существует затычка и для тех дыр, которые изображены на рис. 118,- круглой, квадратной и крестообразной. Она представлена в трех положениях.

74. Существует и такая затычка: вы можете видеть ее с трех сторон на рис. 119.

(Задачи, которыми мы сейчас занимались, приходится нередко разрешать чертежникам, когда по трем «проекциям» какой-нибудь машинной части они должны установить ее форму.)

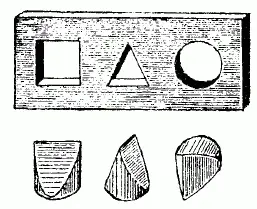
Рис. 117

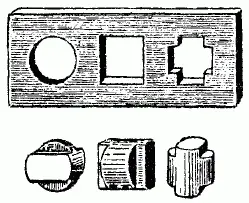
Рис. 118

Рис. 119

75. Как ни странно, но продеть пятак через такое маленькое отверстие вполне возможно. Надо только суметь взяться за это дело. Бумажку изгибают так, что круглое отверстие вытягивается в прямую щель (рис. 120):через эту щель и проходит пятак.

Геометрический расчет поможет понять этот на первый взгляд замысловатый трюк. Диаметр двухкопеечной монеты 18 мм; окружность ее, как легко вычислить, равна 56 мм (с лишком). Длина прямой щели должна быть, очевидно, вдвое меньше окружности отверстия и, следовательно, равна 28 мм. Между тем поперечник пятака всего 25 мм; значит, он может как раз пролезть через 28-миллиметровую щель, даже принимая в расчет его толщину (1 1/ 2мм).

76. Чтобы по снимку определить высоту башни в натуре, нужно прежде всего измерить возможно точнее высоту башни и длину ее основания на фотографическом изображении. Предположим, высота на снимке 95 мм, а длина основания - 19 мм.

Тогда вы измеряете длину основания башни в натуре; допустим, она оказалась равной 14 м.

Сделав это, вы рассуждаете так: фотография башни и ее подлинные очертания геометрически подобны друг другу.