Яков Перельман - Живая математика. Математические рассказы и головоломки

Вы видите, что при известной подготовке и находчивости вы и без мерной линейки можете производить годные для практики измерения.

К этому полезно будет прибавить еще, что наши медные (бронзовые) монеты могут служить при нужде не только масштабом, но и удобным разновесом для отвешивания грузов. Новые, не потертые медные монеты современной чеканки весят столько граммов, сколько обозначено на них копеек [22] К сожалению, современные монеты не отвечают этой закономерности. Можно только надеяться, что и в отношении весов монет будет наведен порядок и мы сможем пользоваться монетами как гирями. – Прим. ред. копеечная монета - 1 г, 2-копеечная - 2 г и т. д. Вес монет, бывших в употреблении, незначительно отступает от этих норм. Так как в обиходе часто не бывает под рукой именно мелких разновесок в 1-10 г, то знание сейчас указанных соотношений может весьма пригодиться.

Для разрешения собранных в этой главе головоломок не требуется знания полного курса геометрии. С ними в силах справиться и тот, кто знаком лишь со скромным кругом начальных геометрических сведений. Две дюжины предлагаемых здесь задач помогут читателю удостовериться, действительно ли владеет он теми геометрическими знаниями, которые считает усвоенными. Подлинное знание геометрии состоит не только в умении перечислять свойства фигур, но и в искусстве распоряжаться ими на практике для решения реальных задач. Что проку в ружье для человека, не умеющего стрелять?

Пусть же читатель проверит, сколько метких попаданий окажется у него из 24 выстрелов по геометрическим мишеням.

Почему передняя ось телеги больше стирается и чаще загорается, чем задняя?

Рис. 96. Какой величины угол, рассматриваемый в лупу?

Угол в 1 1/ 2° рассматривают в лупу, увеличивающую в 4 раза. Какой величины покажется угол (рис. 96)?

Вам знаком, конечно, плотничий уровень с газовым пузырьком (рис. 97),отходящим в сторону от метки, когда основание уровня имеет наклон. Чем больше этот наклон, тем больше отодвигается пузырек от средней метки.

Причина движения пузырька та, что, будучи легче жидкости, в которой он находится, он всплывает вверх. Но если бы трубка была прямая, пузырек при малейшем наклоне отбегал бы до самого конца трубки, т. е. до наиболее высокой ее части. Такой уровень, как легко понять, был бы на практике очень неудобен. Поэтому трубка уровня берется изогнутая, как показано на рисунке. При горизонтальном положении основания такого уровня пузырек, занимая высшую точку трубки, находится у ее середины; если же уровень наклонен, высшей точкой трубки становится уже не ее середина, а некоторая соседняя с ней точка, и пузырек отодвигается от метки на другое место трубки [23] Точнее было бы сказать: «Метка отодвигается от пузырька», потому что пузырек остается на месте, а трубка с меткой скользит мимо него. .

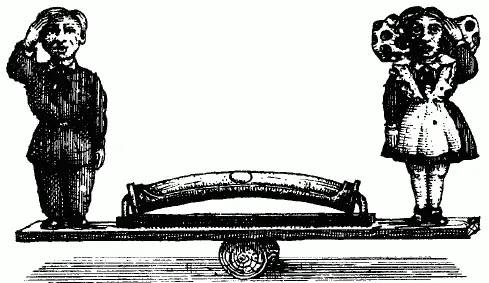
Рис. 97. Плотничий уровень

Рис. 98

Вопрос задачи состоит в том, чтобы определить, на сколько миллиметров отодвинется от метки пузырек, если уровень наклонен на полградуса, а радиус дуги изгиба трубки - 1 м.

Вот вопрос, который, без сомнения, покажется многим слишком наивным или, напротив, чересчур хитроумным.

Сколько граней у шестигранного карандаша?

Раньше чем заглянуть в ответ, внимательно вдумайтесь в задачу.

Фигуру лунного серпа (рис. 98) требуется разделить на 6 частей, проведя всего только 2 прямые линии.

Как это сделать?

Из 12 спичек можно составить фигуру креста (рис. 99),площадь которого равна 5 «спичечным» квадратам. Измените расположение спичек так, чтобы контур фигуры охватывал площадь, равную только 4 «спичечным» квадратам. Пользоваться при этом услугами измерительных приборов нельзя.

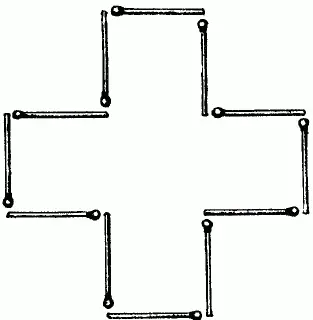
Рис. 99

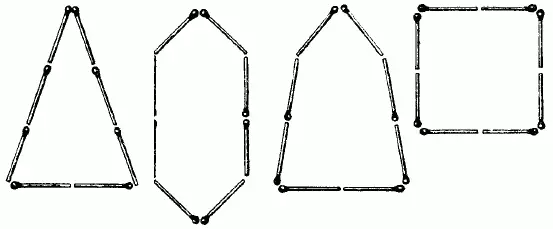
Рис. 100

Из 8 спичек можно составить довольно разнообразные замкнутые фигуры. Некоторые из них представлены на рис. 100;площади их, конечно, различны.

Задача состоит в том, чтобы составить из 8 спичек фигуру, охватывающую наибольшую площадь.

На внутренней стенке стеклянной цилиндрической банки виднеется капля меда в трех сантиметрах от верхнего края сосуда. А на наружной стенке в точке, диаметрально противоположной, уселась муха (рис. 101).

Укажите мухе кратчайший путь, по которому она может добежать до медовой капли.

Высота банки 20 см; диаметр 10 см.

Не полагайтесь на то, что муха сама отыщет кратчайший путь и тем облегчит вам решение задачи: для этого ей нужно было бы обладать геометрическими познаниями, слишком обширными для мушиной головы.

Рис. 101. Укажите мухе кратчайший путь к медовой капле

Перед вами дощечка (рис. 102)с тремя отверстиями: квадратным, треугольным и круглым. Может ли существовать одна затычка такой формы, чтобы закрывать все эти разновидные отверстия?

Рис. 102. Найдите одну затычку к этим трем отверстиям

Если вы справились с предыдущей задачей, то, быть может, вам удастся найти затычку и для таких отверстий, какие показаны на рис. 103?

Наконец, еще задача в том же роде: существует ли одна затычка для трех отверстий (рис. 104)?

Запаситесь двумя монетами современной [24] Монеты достоинством в 5 и 2 коп., имевшие хождение в 1930-е годы, имели следующие размеры: пятак – 2,5 см, двухкопеечная монета – 1,8 см (монеты эти изображены на рис. 94 и 95). – Прим. ред. чеканки: 5-копеечной и 2-копеечной. На листке бумаги сделайте кружок, в точности равный окружности 2-копеечной монеты, и аккуратно вырежьте его.