Яков Перельман - Живая математика. Математические рассказы и головоломки

89,4 х 1000 = 89,4 кг,

потому что килограмм в тысячу раз больше грамма. Далее:

89,4 кг х 1000 = 89,4 т,

потому что тонна в тысячу раз больше килограмма. Итак, искомый вес - 89,4 т.

107. Всех путей по просекам от Адо Вможно насчитать 70. (Систематическое решение этой задачи возможно с помощью так называемого Паскалева треугольника, рассматриваемого в курсах алгебры.)

108. Так как сумма всех чисел, обозначенная на циферблате, равна 78, то числа каждого из шести участков должны составлять вместе 78: 6, т. е. 13. Это облегчает отыскание решения, которое показано на рис. 137.

109-110. Решения показаны на прилагаемых рис. 138и 139.

Рис. 140

111. Трехногий стол всегда может касаться пола концами своих трех ножек, потому что через каждые три точки пространства может проходить плоскость, и притом только одна. В этом причина того, что трехногий стол не качается; как видите, она чисто геометрическая, а не физическая. Вот почему так удобно пользоваться треногами для землемерных инструментов и фотографических аппаратов. Четвертая нога не сделала бы подставку устойчивее; напротив, пришлось бы тогда всякий раз заботиться о том, чтобы подставка не качалась.

112. На вопрос задачи легко ответить, если сообразить, какое время показывают стрелки. Стрелки на левых часах (рис. 140)показывают, очевидно, 7 час. Значит, между концами этих стрелок заключена дуга в 5/ 12полной окружности.

В градусной мере это составляет

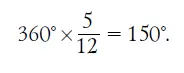
Стрелки на правых часах показывают, как нетрудно сообразить, 9 ч 30 мин. Дуга между их концами содержит 3 % двенадцатых доли полной окружности, или 7/ 24.

В градусной мере это составляет

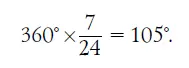
113. Принимая рост человека в 175 см и обозначив радиус Земли через R, имеем:

2 х 3,14 х (R + 175) - 2 х 3,14 х R = 2 х 3,14 х 175 = 1099 см,

т. е. около 11 м.

Рис. 141

Поразительно здесь то, что результат совершенно не зависит от радиуса шара и, следовательно, одинаков на исполинском Солнце и маленьком шарике.

114. Требование задачи легко удовлетворить, если расставить людей в форме шестиугольника, как показано на рис. 141.

115. На рис. 142указаны следы сабельных ударов, а на рис. 143видно, как надо расположить образовавшиеся 4 куска, чтобы составить второй, более характерный символ фашистской диктатуры: квадрат концентрационного лагеря.

Рис. 142

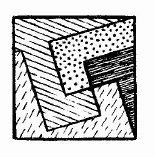
Рис. 143

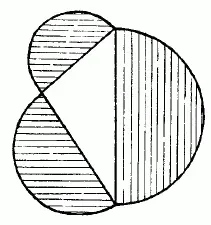
Рис. 144

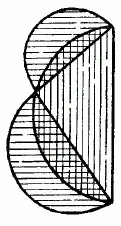
Рис. 145

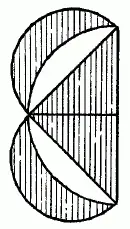
Рис. 146

116. Читатели, слыхавшие о неразрешимости задачи квадратуры круга, сочтут, вероятно, и предлагаемую задачу неразрешимой строго геометрически. Раз нельзя превратить в равновеликий квадрат полный круг, то, думают многие, нельзя превратить в прямоугольную фигуру и луночку, составленную двумя дугами окружности. Между тем задача, безусловно, может быть решена геометрическим построением, если воспользоваться одним любопытным следствием общеизвестной Пифагоровой теоремы.

Следствие, которое я имею в виду, гласит, что сумма площадей полукругов, построенных на катетах, равна полукругу, построенному на гипотенузе (рис. 144).Перекинув большой полукруг на другую сторону (рис. 145).видим, что обе заштрихованные луночки вместе равновелики треугольнику [38] Положение это известно в геометрии под названием «теоремы о Гиппократовых луночках». .

Если треугольник взять равнобедренный, то каждая луночка в отдельности будет равновелика половине этого треугольника (рис. 146).

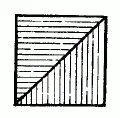
Рис. 147

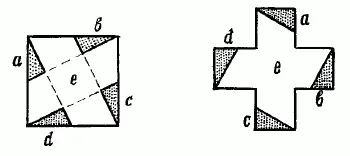
Рис. 148. Превращение квадрата в крест

Отсюда следует, что можно геометрически точно построить равнобедренный прямоугольный треугольник, площадь которого равна площади серпа. А так как равнобедренный прямоугольный треугольник легко превращается в равновеликий квадрат (рис. 147)»то и серп наш возможно чисто геометрическим построением заменить равновеликим квадратом.

Остается только превратить этот квадрат в равновеликую фигуру Красного Креста (составленную, как известно, из 5 примкнутых друг к другу равных квадратов). Существует несколько способов выполнения такого построения; два из них показаны на рис. 148и 149.

Оба построения начинают с того, что соединяют вершины квадрата с серединами противоположных сторон. Важное замечание: превратить в равновеликий крест можно только такую фигуру серпа, которая составлена из двух дуг окружностей: наружного полукруга и внутренней четверти окружности соответственно большего радиуса [39] Тот лунный серп, который мы видим на небе, имеет несколько иную форму: его наружная дуга – полуокружность, внутренняя же – полуэллипс. Художники часто изображают лунный серп неверно, составляя его из дуг окружностей. .

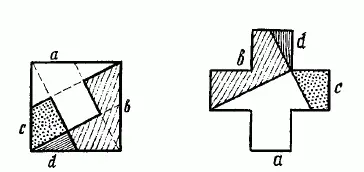
Рис. 149. Другой способ превращения квадрата в крест

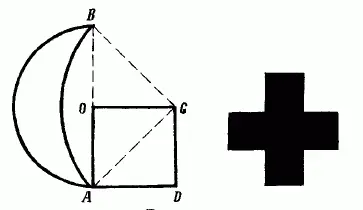
Рис. 150

Итак, вот ход построения креста, равновеликого серпу. Концы Аи Всерпа (рис. 150)соединяют прямой: в середине О этой прямой восставляют перпендикуляр и откладывают ОС=ОА.Равнобедренный треугольник ОАСдополняют до квадрата ОАDС,который превращают в крест одним из способов, указанных на рис. 148и 149.

117. Приводим окончание прерванного рассказа Бенедиктова: