Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Увлечь и позабавить человечество с помощью приспособления, которое выдает результаты, не поддающиеся контролю.

Мы начинаем с класса персонажей, известных под названием «люди». Эти существа любят все контролировать, поэтому они изобрели автомобили, оружие, правительства и центральное кондиционирование. Но они одержимы еще и тем, что находится вне их контроля: пробки на дорогах, погода, их дети и успехи известных парней, которые занимаются спортом за деньги.

В глубине сердца люди хотят противостоять судьбе, держать свое бессилие в собственных ладонях. Так возникают игральные кости — карманные частицы судьбы.

В VI тысячелетии до н. э. племена Древней Месопотамии использовали в качестве игральных костей камни и ракушки. Древние греки и римляне предпочитали овечьи бабки. Индейцы — бобровые зубы, скорлупу грецкого ореха, вороньи когти и сливовые косточки. В санскритском эпосе Древней Индии цари кидали пригоршни орехов бибхитаки. Эти природные игральные кости позволяли резаться в азартные игры, предсказывать судьбу, делить добычу и (вне всяких сомнений) были неотъемлемой частью других ритуалов, от священных до повседневных. Как десерты и послеобеденный сон, идея игральных костей была настолько очевидна и красива, что каждая культура приходила к ней независимо от других.

В наши дни лишь горстка ярых консерваторов играет в «Монополию», бросая бобровые зубы. Цивилизация продвинулась от найденных где попало игральных костей к спроектированным.

А теперь начинается настоящая игра в кости.

Когда вы бросаете игральную кость, вероятность выпадения каждой грани должна быть одинаковой. В противном случае соперники нервничают, становятся подозрительными и перестают приглашать вас на вечеринки, где играют в нарды.

Полезная отправная точка: конгруэнтность . Две геометрические фигуры называют конгруэнтными, если одну можно наложить на другую так, чтобы они совпали. Конгруэнтные геометрические фигуры — неотличимые близнецы, углы и стороны одной равны соответствующим углам и сторонам другой. Таким образом, первая идея проектирования честной игральной кости — убедитесь, что все грани конгруэнтны друг другу .

Звучит отлично… пока не встретишься с курносым дисфеноидом.

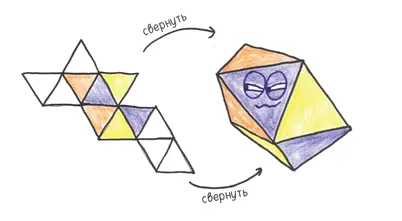
Этот полиэдр, многорылый слепыш, развенчивает наши надежды. Все его 12 граней — идентичные друг другу равносторонние треугольники. Но эту игральную кость нельзя назвать честной [56] У курносого дисфеноида есть два кузена: грани этих полиэдров — равносторонние треугольники, но одни грани все равно будут выпадать чаще, чем другие: (1) трижды наращенная треугольная призма (спасибо за подсказку Лоуренсу Рэкхему) и (2) скрученно удлиненная четырехугольная бипирамида (спасибо за подсказку Тиму Кроссу и Питеру Оллису). Если вы предпочитаете четырехугольные грани, есть и (3) псевдодельтоидальный икоситетраэдр (спасибо за подсказку Александру Мюницу). .

В некоторых его вершинах пересекаются четыре треугольника, а в прочих — пять треугольников. Когда вы кидаете на стол этого маленького монстра, некоторые грани выпадают чаще, чем другие. Боюсь, что конгруэнтности граней недостаточно.

Нам нужна симметрия .

Говоря простым языком, симметрия означает неуловимое, ласкающее глаз единообразие.

Ее математический смысл гораздо конкретнее: геометрическое действие, преобразующее объект, но не меняющее его сути. Например, у квадратного стола есть восемь видов симметрии:

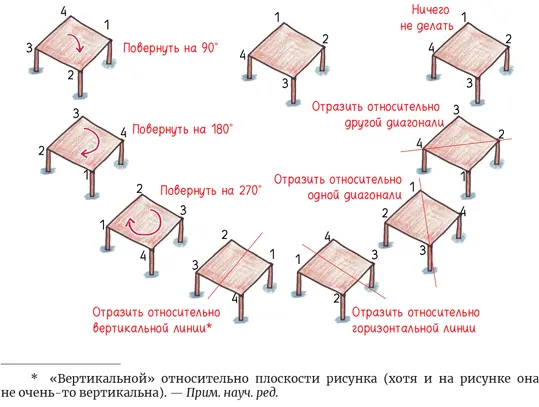
Симметрические отображения не меняют форму стола, однако внимательный анализ показывает, что они меняют местами его углы. Например, поворот на 180º меняет местами противоположные углы: № 1 занимает место № 3, и то же самое с № 2 и № 4. Сравните с отражением по диагонали, которое меняет местами углы № 2 и № 4, но оставляет на своих местах углы № 1 и № 3. Симметрические отображения игральной кости работают примерно так же: грани меняются местами, но форма остается неизменной.

Симметрия предлагает верный путь к честной игре. Просто выберите геометрическое тело, достаточно симметричное, чтобы все грани можно было поменять местами.

Например, бипирамида. Возьмите две идентичных пирамиды и приклейте их основания друг к другу. Правильная комбинация поворотов сможет поменять любую треугольную грань на любую другую, и это означает, что все грани геометрически эквивалентны и игральная кость честная.

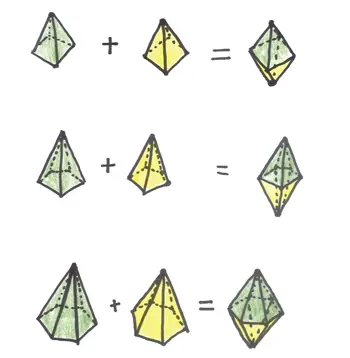
Другой пример: трапецоэдр. Он выглядит как бипирамида {32} 32 Его иногда называют косая бипирамида . — Прим. науч. ред. с изящной резьбой по экватору, которая превращает треугольники в четырехугольники, похожие на воздушных змеев.

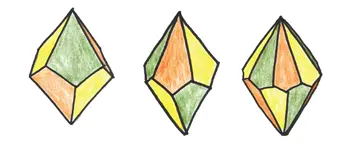
Вы можете сделать бипирамиду или трапецоэдр с любым количеством граней: 8, 14, 26, 398 {33} 33 С любым четным, начиная с 6. Кстати, куб — это частный случай шестигранного трапецоэдра. — Прим. науч. ред. . Теоретически любая из этих игральных костей обеспечит честную игру, грани будут выпадать с одинаковой вероятностью. Наверное, вы думаете, что мы решили проблему. Игра в кости окончена, да? Не так быстро! Люди гораздо капризнее. Недостаточно, чтобы игральная кость была честной…

Мы встретились с номинантами на роль игральной кости, которые (1) легко поддаются определению, (2) дают справедливые результаты и (3) носят потрясающие греческие и латинские именами. Однако эти многообещающие модели — стопроцентные исторические неудачники, провалившиеся кандидаты в президенты мира случайности. Насколько я знаю, ни одна цивилизация, играющая в кости, не пользовалась бипирамидой и есть всего один пример использования трапецоида: теневое сообщество фанатов настольной игры «Подземелья и драконы», где используют десятигранный трапецоид (d10) {34} 34 В играх на придумывание сюжетов иногда используют 14-гранный трапецоэдр, чтобы задать день недели. — Прим. науч. ред. .