Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Кинг-Конг, горилла размером с трехэтажный дом. Поль Баньян {26} 26 Персонаж канадского фольклора. — Прим. пер. , лесоруб, который мог перешагивать озера. Шакил О’Нил, легендарный баскетболист ростом 213 см и весом 147 кг, которому дается все, кроме штрафных бросков. Вы знаете эти истории, и вы прекрасно понимаете, что все это фантазии, легенды, наивные выдумки. Великанов не существует [46] Впервые я узнал об этом в колледже из курса Лори Сантос «Секс, эволюция и человеческая природа». Нет, я, конечно, уже знал, что великанов не существует, но объяснения профессора Сантос (возможно, как я сейчас вижу, вдохновленные Холдейном) помогли сформировать костяк этой главы. .

Почему? Потому что размер имеет значение.

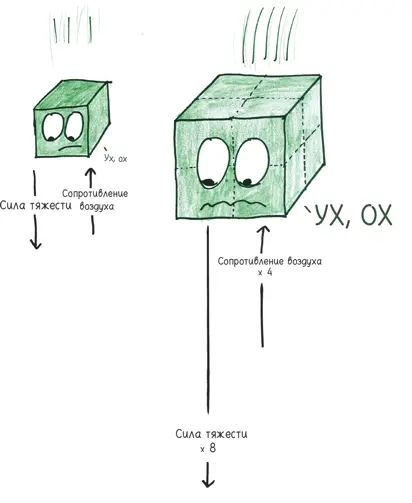
Предположим, мы возьмем в качестве образцового человеческого экземпляра Дуэйна Джонсона {27} 27 Американский рестлер и киноактер ростом около 2 м. — Прим. пер. и удвоим его размеры. Если мы удвоим его вдоль, поперек и в высоту, общая масса тела Дуэйна вырастет в восемь раз.

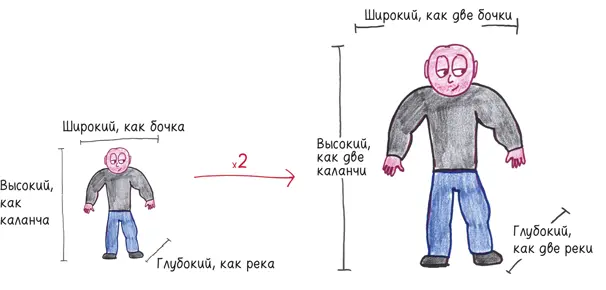
Пока все в порядке. Но взгляните на его ноги. Чтобы он не падал, кости должны быть в восемь раз сильнее. Могут ли они выдержать его вес?

Сомневаюсь. Два удвоения были полезны (вдоль и поперек), но одно бесполезно: в высоту. Вы не делаете колонну крепче, удваивая ее высоту, и точно так же нога не становится сильнее, если удлиняется. Дополнительная высота не дает дополнительной прочности, просто увеличивает нагрузку, и кости сломаются под весом гигантского тела.

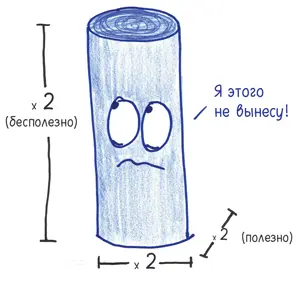
Ноги Дуэйна не угонятся за предъявленными требованиями: умножение на 4 не соответствует умножению на 8. Если мы будем продолжать увеличивать Дуэйна Джонсона, удваивая, утраивая и учетверяя его размеры, в конце концов он достигнет критической точки. Кости ног согнутся и треснут под сокрушительным весом туловища [47] Пожалуйста, дозвонитесь до ваших сенаторов и убедите их профинансировать жизненно важные объекты инфраструктуры Дуэйна Джонсона, пока не стало слишком поздно. .

Этот процесс называется изометрическим масштабированием : увеличение фигуры при сохранении ее пропорций («изо−» означает «одинаковый»). Никудышный метод для создания больших животных. Вместо него нам нужно аллометрическое масштабирование : увеличение фигуры с изменением пропорций («алло−» означает «другой»).

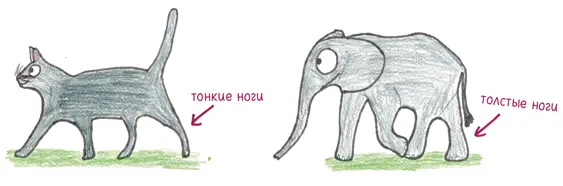
Если мы увеличим рост животного на 50 %, его ноги справятся с нагрузкой, только если станут на 83 % толще. Вот почему кошки могут выжить со стройными лапами, а слонам нужны ноги-столбы, чтобы не упасть.

Ограничение, наложенное на рост Дуэйна Джонсона, распространяется на всех нас, поэтому великаны живут только в сказочных царствах. Берцовые кости Поля Баньяна трескались бы с каждым шагом через озеро. Мускулы Кинг-Конга никогда не смогли бы вынести его массу: сила мускулов была бы больше в r2 раз, чем у обычной гориллы, а масса — в r3 раз. Он бы так и не сдвинулся с места: гигантская горилла-размазня, страдающая сердечной недостаточностью. А как насчет Шакила О’Нила? Ну, его история настолько неправдоподобна, что, мне кажется, вряд ли кто-нибудь на самом деле в нее верит.

Муравьи вселяют ужас. Они поднимают предметы, в 50 раз превышающие массу их тельца, работают сообща с безукоризненной координацией действий и живут припеваючи во всех уголках нашей планеты.

Эта глобальная армия тяжелоатлетов-телепатов, вооруженных жвалами, превосходит человечество по численности в миллион раз. Фантомы их инопланетных морд мешали бы мне спать спокойно, если бы не один спасительный факт.

Муравьи очень, очень малы.

Пришло время закрепить материал, усвоенный в предыдущих баснях. Когда линейные размеры фигуры растут, площадь ее поверхности растет гораздо быстрее, а объем растет еще быстрее.

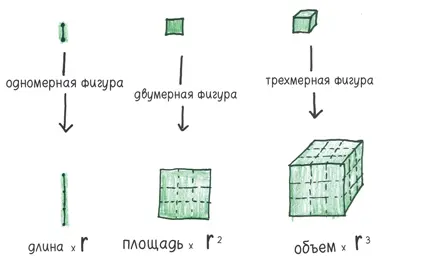
Это означает, что у больших тел (например, человеческих) больше объема на единицу площади поверхности. У маленьких тел (например, муравьиных) все наоборот. У наших заклятых врагов большая площадь поверхности на единицу объема.

Каково это — иметь меньше объема на единицу площади поверхности? Прежде всего это означает, что вам никогда не нужно бояться высоты.

Когда вы падаете с большой высоты, две силы играют в перетягивание каната: сила тяжести тянет вас вниз, сопротивление воздуха удерживает. Сила тяжести зависит от массы, поэтому ее величина зависит от вашей плотности и объема. Сопротивление воздуха зависит от площади поверхности вашего тела.

Короче говоря, ваша масса ускоряет падение, а площадь поверхности замедляет. Поэтому кирпичи стремительно падают вниз, а бумажные листы порхают; орлы парят, а пингвины не могут летать [48] Математика сопротивления воздуха лежит в основе еще одной короткой басни: «Зачем большим кораблям огромные паруса». Когда вы удваиваете размеры вашего корабля, его площадь (2D) учетверяется, но масса (3D) увеличивается в восемь раз. Вы будете ловить относительно меньше ветра, если не измените пропорции. Поэтому, если корабль в два раза длиннее, его мачты примерно в три раза выше. .

Мы с вами похожи на пингвинов: большая масса, небольшая площадь поверхности. В процессе падения мы разгоняемся до предельной скорости почти 193 км/ч, и соприкосновение с землей довольно неприятно {28} 28 Сопротивление воздуха зависит не только от площади, но и от скорости, поэтому скорость соприкосновения с землей практически не зависит от высоты, если эта высота достаточно велика. — Прим. науч. ред. .

Муравьи же похожи на орлов, только бумажных: большая площадь поверхности, небольшая масса. Их предельная скорость равна 6,4 км/ч. Теоретически муравей мог бы спрыгнуть с Эмпайр-стейт-билдинг, приземлиться на все свои шесть ножек на тротуар и пойти по своим делам, напевая «Муравьиный марш».

Итак, если у вас меньше объема на единицу площади поверхности, можно вволю предаваться играм, развлечениям и скайдайвингу без парашюта? Разумеется нет. У муравьев свои горести, и под горестями я имею в виду изнурительную и всецело оправданную водобоязнь.