Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Гвен . Есть всего один способ это выяснить.

Решительным движением Гвен складывает лист бумаги пополам и помечает три размера: длинный (длина изначального листа), средний (ширина изначального листа) и короткий (ширина половины листа).

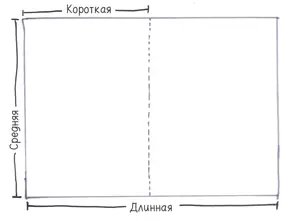
Гвен (продолжая операции с бумагой) . Итак, каково соотношение между длинным и средним?

Свен . Это именно то, что мы пытаемся выяснить.

Гвен . Хорошо, каково соотношение между средним и коротким?

Свен . Черт возьми, Гвен! Мы знаем, что соотношение такое же, но мы до сих пор не знаем, чему оно равно.

Проходит мгновение, исполненное романтического напряжения.

Гвен . Окей. Допустим, средняя сторона в r раз длиннее короткой.

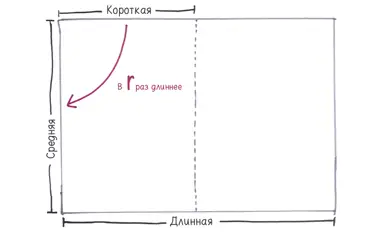
Свен . Но чему равно r ?

Гвен . Пока не знаю. Все, что я знаю, — оно больше одного, но меньше двух, потому что средняя сторона длиннее, чем короткая, но не вдвое длиннее.

Свен . Ну хорошо. Полагаю, длинная сторона тоже в r раз длиннее средней.

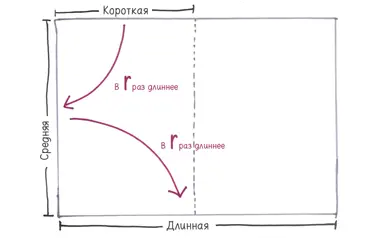
Гвен . Следовательно, если ты хочешь узнать длину длинной стороны, зная длину короткой, ее надо умножить на r (чтобы узнать длину средней) и снова на r . Получается r в квадрате.

Свен (бьет кулаком по столу) . Ты двужильный гений, ты великан среди карликов! Гвен, получилось!

Гвен . Неужели?

Свен . Длинная сторона в r2 длиннее короткой. Но погляди: она же в два раза длиннее короткой!

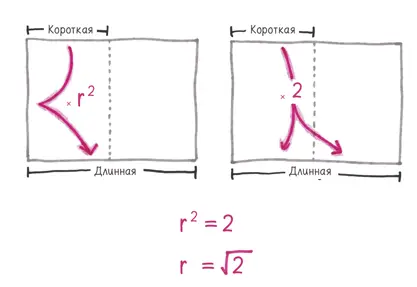
Гвен . Слов нет… ты прав… и это означает…

Свен . Да, r2 равно 2.

Гвен . Поэтому r равно квадратному корню из двух! Это и есть секретное соотношение, которое положит конец всем мучениям и объединит человечество!

Свен (внезапно с другим акцентом). Прекрасно, Гвен. Уступи мне это число.

Гвен . Свен? Зачем ты достал пистолет?

Я заблуждался: создатели формата А4 выбрали соотношение сторон не для того, чтобы насолить лично мне. Они выбрали его и не по сиюминутному капризу, и не в знак упорного противостояния американской гегемонии, и не из садистского удовольствия подобрать иррациональное число.

На самом деле они его в принципе не выбирали.

Они решили создать систему бумажных форматов, каждый из которых вдвое меньше предыдущего. Это довольно крутой и труднодостижимый трюк. Но когда они вступили на этот путь, решение перестало зависеть от их выбора. Есть всего одно число, отвечающее поставленным требованиям, и так уж вышло, что это и есть знаменитое иррациональное число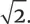

Теперь я знаю, что всем нам нравится воображать дизайнеров бумаги необузданными фантазерами, ограниченными только пределами своего воображения. Но в действительности все намного интереснее. Дизайнеры движутся в пространстве возможностей, которыми управляют логика и геометрия. Это застывший ландшафт: некоторые числа рациональны, другие нет, и ни один дизайнер ничего не может тут поделать. Вместо этого он должен лавировать среди этих препятствий — или, что даже лучше, превратить их в преимущества, как архитектор, чье здание гармонирует с окружающей средой.

Короче говоря, не буду долго разглагольствовать: я поменял свое мнение о формате А4. Теперь, когда я знаю, почему соотношение сторон стремится к 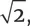тот факт, что производители бумаги обречены на микроскопическую ошибку, меня больше не тревожит. Честно говоря, формат А4 даже перестал казаться мне неправильным. Теперь меня, наоборот, раздражает бумага формата US Letter, слегка располневшая и старомодная.

Кажется, я завершил переход из одной категории несносных американцев в другую. Из шовиниста и поборника моих своевольных национальных обычаев я стал страстным проповедником зарубежных традиций. Сейчас я даже реже пью карамельные коктейли, хотя уверен, что полностью никогда не откажусь от них, как и от бумаги американского формата.

У басен много общего с математикой. И те и другие пришли из пыльных, изъеденных молью книг. Их навязывают детям. И они пытаются объяснить мир с помощью радикальных упрощений.

Если вы хотите познакомиться со всей причудливостью и сложностью жизни, оглядитесь вокруг. Поговорите с биологом, или художником-реалистом, или с кем-нибудь, кто собирает документы для уплаты налогов. Баснописцы и математики скорее сродни карикатуристам. Педалируя одни черты и пренебрегая всеми остальными, они помогают объяснить, почему наш мир таков, каков он есть.

Эта глава — небольшое собрание математических басен. Они показывают, как разные области, от кулинарии до биологии и финансирования искусства, подчиняются законам геометрии. В основе этих басен лежит одна основная идея, мораль настолько простая, что даже Эзоп не проговаривал ее вслух: размер имеет значение [42] Когда я работал над этой главой, мой коллега и образец для подражания Ричард Бриджес указал мне на прекрасное изложение тех же идей в эссе 90-летней давности. Я многое позаимствовал оттуда: J. B. S. Haldane, «On Being the Right Size», март 1926, https://irl.cs.ucla.edu/papers/right-size.pdf . .

Большая статуя — не просто увеличенная версия маленькой статуи. Это совершенно иной объект.

Мы с вами любим печь торты. Мы с гордостью месим тесто, чтобы осчастливить человечество шоколадным чудом. Духовка уже нагревается, но когда мы открываем кухонный шкаф, то неожиданно обнаруживаем, что наша форма для выпечки в два раза длиннее и шире, чем указано в рецепте из поваренной книги [43] Я пренебрегаю высотой, потому что при готовке шоколадных тортов вы никогда не заполняете форму тестом доверху. .

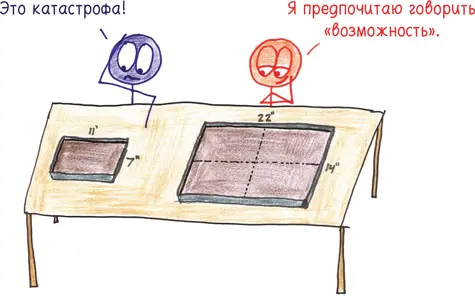
Что же нам делать?

Для того чтобы заполнить эту удвоенную форму для выпечки, у нас есть искушение взять в два раза больше ингредиентов. Но на самом деле это полумера. Посмотрите внимательнее, и вы поймете: нам необходимо учетверить количество ингредиентов.