Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Ферменная конструкция Уоррена, появившаяся в 1848 году, задействовала равносторонние треугольники.

Балтиморские и пенсильванские ферменные конструкции — вариации ферм Пратта со вложенными треугольниками — стали повсеместно использовать при строительстве железнодорожных мостов.

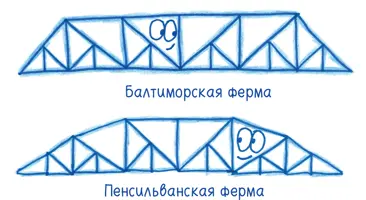
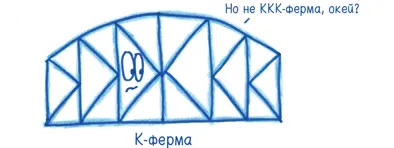
K-ферма комбинирует разные виды треугольников (надеюсь, никому не приходит на ум ку-клукс-клан).

Ферменная конструкция Бейли стала использоваться во время Второй мировой войны. В соответствии с теми или иными военными нуждами унифицированные модульные треугольники могли быть разобраны, погружены на корабли и снова собраны.

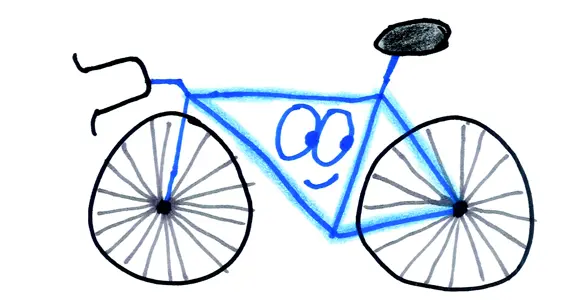
Речь идет не только о мостах. Треугольные крыши тоже нуждаются в ферменных конструкциях — стропилах. С их помощью делают скелет высотных зданий. Чего уж там, стандартная велосипедная рама — не что иное, как простейшая ферма из двух треугольников. В современном городе вы перемещаетесь среди треугольников, они вас поддерживают, вы даже ездите на них.

Архитекторы скованы мириадами ограничений: бюджет, строительные нормы, законы физики. Они прибегают к помощи треугольников не из эстетических соображений, как художники или оформители интерьеров, а потому, что в мире геометрии нет других квалифицированных кандидатов. Брак между архитектурой и треугольниками заключен не по любви. В лучшем случае — ради удобства, в худшем — от безысходности. Таким образом, можно ожидать, что конструкции будут получаться ошарашивающими — как последний отчаянный компромисс, как бельмо на глазу.

И все же они прекрасны. Забавный парадокс дизайна: полезность порождает красоту. В эффективности есть элегантность. Приятно смотреть на вещи, которые просто-напросто функционируют.

Думаю, то же удовольствие я получаю от математики. Хороший математический аргумент, как и хорошо сконструированная ферма, просто-напросто функционирует. Уберите один основополагающий постулат, и все придуманное вами рухнет. Здесь есть неоспоримая грация: минимализм, поддерживающие друг друга элементы, абсолютная прочность и ни единой лишней унции.

Я не могу объяснить, почему те или иные вещи кажутся мне прекрасными. (Скажем, поп-рок девяностых.) Но я знаю, что в повествовании о треугольнике есть нечто превосходное. Трехсторонность делает его уникальным; уникальность, в свою очередь, делает его могущественным; могущество же делает его ключевым элементом современной архитектуры. Возможно, есть натяжка в утверждении о том, что треугольник «спасает мир», но, если вам интересно мое мнение, он делает мир лучше. Треугольник позволил миру стать таким, какой он есть.

По прибытии в Англию [38] Благодарю Кэролайн Гиллоу и Джеймса Батлера (чьи души настолько велики, что разделяющий нас Атлантический океан выглядит просто лужицей) за помощь и поддержку при написании этой главы и за то, что опыт пребывания в Англии был настолько замечательным. я был готов столкнуться с огрехами моего американского воспитания. Вместо научных градусов Цельсия я пользовался архаичными градусами Фаренгейта. Вместо аккуратных километров (состоящих из 1000 метров) я использовал причудливые мили (состоящие из 5280 футов). Вместо чая я заливал в свой топливный бак карамельные коктейли, будучи верен бренду «Старбакс». И я заранее знал, что мне непросто дастся адаптация к традициям цивилизованного мира.

Но был один культурный шок, который я не предвидел: форматы бумаги.

Как все янки, я вырос, используя бумагу формата US Letter: 8,5 дюймов (21 3/ 5см) в ширину и 11 дюймов (27 19/ 20см) в длину, поэтому иногда этот формат называют броским именем — поистине убийственный брендинг — «восемь с половиной на одиннадцать». Если бы я пораскинул мозгами, то понял бы, что в других странах вместо дюймов ведут измерения в сантиметрах, поэтому формат US Letter им вряд ли подойдет.

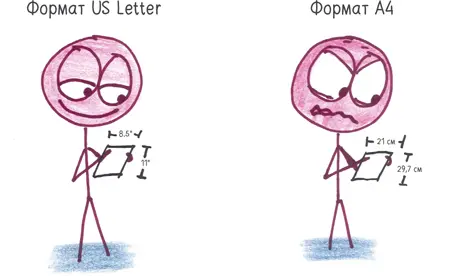
Название «восемь с половиной на одиннадцать» представляется мне неуклюжим, но оно меркнет на фоне ужасного словосочетания «двадцать один и три пятых на двадцать семь и девятнадцать двадцатых».

Когда же я увидел листки их формата — известного под еще менее привлекательным названием «A4» — я испытал к ним острое отвращение. Они слишком узкие, как модные джинсы. Я давно привык к свободному крою типа клеш, и все мое существо раздражала эта изящная европейская белиберда. Длина бумаги формата US Letter примерно на 30 % больше ее ширины; очевидно, что в Европе соотношение было иным. И, что столь же очевидно, оно было хуже.

Поэтому я решил присмотреться к размерам бумаги A4. Я предполагал что-то вроде 22,5 см на 28 см или, возможно, 23 см на 30 см.

Мило и аккуратно с точки зрения этих европейцев, помешанных на метрической системе мер, не правда ли?

А вот и нет. Верный ответ: 21 см на 29,7 см.

Какого черта?

Я поделил 29,7 на 21, чтобы выяснить упрощенное соотношение: примерно 1,41. Будучи учителем математики, я сразу же узнал это число: оно (приблизительно) равно 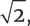иначе говоря, квадратному корню из двух. И если раньше я недоумевал, то теперь мгновенно зарычал и воспылал негодованием.

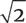— иррациональноечисло: то есть оно не является соотношением двух целых чисел.

Производители бумаги выбрали иррациональную пропорцию, которая — я не стану деликатничать — вообще вне всякого рацио .

Как правило, в жизни мы пользуемся двумя видами чисел: (1) целыми числами, например: «У меня трое детей», «Каждое утро мои дети съедают пять тарелок каши» и «Спектр пятен на одежде моих детей — более 17 цветов»; (2) соотношениями целых чисел, например: «Мы тратим ¼ семейного дохода на конструктор „Лего“», «Дома, где живут дети, в 17½ раз чаще разрисованы фломастером», «Эй, когда успели поседеть ⅔ моих волос?».