Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Поэтому забудьте сентиментальную фразу «Все возможно»! Да, это мило, но глубоко противоестественно, как и многие другие вещи, которые мы скармливаем детям. Реальность строже — и удивительнее.

Хочу познакомить вас со звездой этой главы — треугольником.

Это не привычный для вас протагонист. Высокомерные литературные типажи могут сбросить его со счетов, потому что он слишком плоский. Тем не менее этот нетипичный герой предпримет типичное героическое путешествие: родившись в убогой семье, научится применять внутреннюю силу и в конце концов сослужит службу всему миру в кризисные времена.

Теперь, если ваше сознание настолько зашорено, что вы не можете вместить идею доблестного многоугольника, ни в коем случае не читайте дальше. Наденьте глазную повязку предрассудков. Но, убедительно прошу вас, зажмурьтесь достаточно крепко, ибо лишь глубочайшая тьма сможет укрыть ваше сумеречное сознание от сияющей истины, пронзительного света плоской геометрии. Разве вы забыли? Мы возвели этот город. Мы возвели этот город на треугольниках…

Добро пожаловать в Древний Египет: процветающее царство, засилье чиновников, строгая вера и локти, согнутые под прямым углом. Оно просуществует несколько тысячелетий и переживет восход и закат империй с властелинами в коронах поскромнее.

Идем, подышим свежим воздухом. На дворе 2570 год до н. э., и Великая пирамида Гизы уже построена наполовину [30] Необходимо отметить основной источник этой главы: Mario Salvadori, Why Buildings Stand Up (New York: W. W. Norton, 1980). Великолепная, внятная книга, без которой эта глава была бы шаткой, как ошибочное доказательство. Кроме того, я благодарен за помощь при написании этой главы Уиллу Уонгу, архитектору мысли и победителю университетских спортивных турниров. . Три с половиной миллиона тонн кирпичей возвышаются среди пустыни, и на них взгромоздят еще три миллиона тонн. Самые тяжелые блоки весят больше двух слонов. Основание представляет собой квадрат со стороной 230 м (протяженность трех кварталов Нью-Йорка). Когда спустя десять лет пирамида будет закончена и 80 000 рабочих смогут расслабиться и выпить лимонаду, высота пирамиды будет составлять 150 м. Через пять тысячелетий она по-прежнему будет целехонька — самый непоколебимый небоскреб в истории человечества, величайший триумф триангулярной архитектуры.

Но на самом деле все не так.

Не поймите меня превратно: она еще не рухнула (по крайней мере, по моим последним данным). Но это никакая не победа треугольников. Если вы желаете увидеть треугольники в деле, забудьте о Великой пирамиде и прогуляйтесь со мной до пустыря неподалеку. Там мы обнаружим небольшую команду землемеров с канатом, завязанным странной петлей с 12 узлами на равном расстоянии друг от друга [31] Я узнал о египетских вязальщиках узлов из книги: Kitty Ferguson, Pythagoras: His Lives and the Legacy of a Rational Universe (London: Icon Books, 2010). .

Зачем? Просто понаблюдайте. Сделав несколько шагов, каждый третий землемер берет свой узел (№ 1, № 4 и № 8, если быть точным), и они натягивают канат. Словно по волшебству, он образует прямоугольный треугольник. Четвертый рабочий отмечает прямой угол на песке. Землемеры ослабляют натяжение каната. Эта сценка повторяется снова и снова, пока весь пустырь не будет поделен на идеальные участки равного размера.

Если вы не клевали носом на уроках геометрии (и даже если клевали), эта сценка, возможно, вызовет в памяти теорему Пифагора. Ее формулировка такова: если вы построите по квадрату на сторонах прямоугольного треугольника, сумма площадей двух меньших квадратов будет равна площади большего. Или, говоря современным алгебраическим языком: а 2+ b 2= с 2.

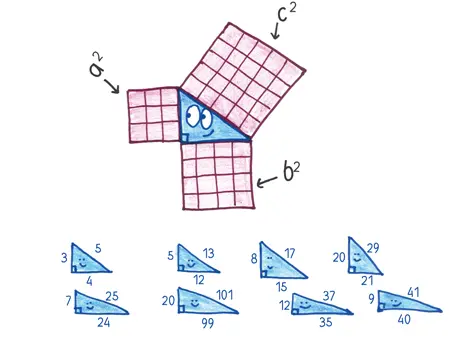
Реестр таких треугольников бесконечен. Например, длины сторон могут быть равны 5, 12 и 13; или 7, 24 и 25; или 8, 15 и 17; или (мой любимый пример) 20, 99 и 101. Египтяне мудро выбрали простейший случай: треугольник со сторонами 3, 4 и 5. Вот поэтому узлов именно 12.

Но эта глава не о Пифагоре и «его» теореме (которую и без его помощи знали более древние цивилизации). Она о более простом и фундаментальном свойстве треугольников, замаскированном изяществе, которое мы скоро обнаружим. История треугольника начинается не в пифагорейском храме и не на вершине Великой пирамиды, а здесь, на пустыре. Канат превращается в инструмент землемера. Это первый увиденный нами намек на столь могущественную силу, что по сравнению с ней пирамиды — просто пригоршня пыли.

Психологическая фаза в процессе нашего рассказа! Треугольник должен вглядеться в собственную душу и задаться заветным вопросом: «Кто есмь аз?»

— Я фигура, подобная прочим, ничем не отличимая от них, за исключением количества сторон и углов?

Музыка звучит все громче, и треугольник молит космос о знаке, цели, озарении.

— О, из чего, — он вопиет, — на самом деле создан я?

Глас громовой грохочет из глубин.

— Я создан из трех сторон.

Окей, возможно, здесь нет такого откровения, как в моментах самопостижения. Немного похоже на то, как пациент психотерапевта замечает, что лежит на кушетке. Но здесь есть потаенные бездны. Нам откроется новая истина, если мы увидим в треугольнике не просто цельную фигуру, а совокупность трех частей.

Например: для создания треугольника сгодятся не любые три отрезка. Возьмем длины 10, 3 и 2 см. Эти три отрезка образуют этакую недофигуру с зазором — недотреугольник, если вам угодно. Длинный отрезок слишком длинный; короткие слишком коротки. Я окрещу его «Треугольник Ти-рекс», потому что короткие передние лапки не соответствуют массивному туловищу.

Это универсальная истина: самая длинная сторона треугольника должна быть короче, чем сумма двух других.

Это правило совершенно очевидно для мухи, ползущей по периметру треугольника. Ей известно, что путь напрямик (от A до B) всегда будет короче, чем обходной путь (от A до B, минуя C). Таким образом, сумма двух коротких сторон должна быть больше, чем длина третьей стороны.