Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

Есть лишь одна проблема: балки неэффективны.

Архитектура, как и сама жизнь, вся строится на управлении напряжением. В то время как жизнь напрягает нас разнообразно (дедлайны, воспитание детей, разряжающийся телефон и т. д.), строительная конструкция испытывает всего два вида напряжений: растяжение и сжатие. Растяжение удлиняет объект, сжатие — укорачивает. Каждый вид напряжения имеет свои особенности, и разные материалы выдерживают их по-разному. Бетон может выдерживать фантастические степени сжатия, но при растяжении крошится. С другой стороны, стальные тросы могут выдержать невероятное растяжение, но прогибаются при малейшем сжатии.

А теперь представьте, что балка проседает под нагрузкой. Она выгибается в улыбку (или скорее гримасу). Какова природа этой деформации — растяжение или сжатие?

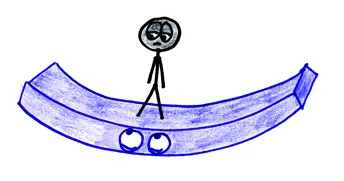
Ответ: и то и другое. Посмотрите на верхнюю часть балки: она становится короче нижней; так бегун на той круговой дорожке, что ближе всего к центру стадиона, преодолевает наименьшее расстояние. Таким образом, ее материал подвергается сжатию. Теперь взгляните вниз; вспомните, что бегун на самой дальней дорожке от центра преодолевает наибольшее расстояние; так и нижняя часть балки становится длиннее верхней части, и, таким образом, ее материал испытывает растяжение.

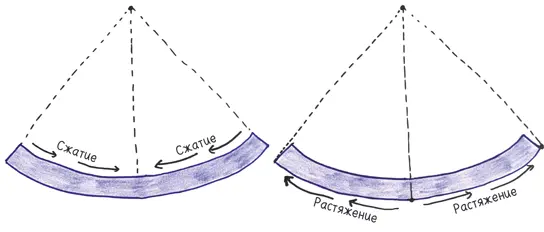
Все еще не о чем тревожиться: многие материалы, такие как дерево, легко выдерживают и растяжение, и сжатие. Проблема не в том, что на балку действует два вида напряжения; проблема в том, что бóльшая часть балки не испытывает никакого напряжения.

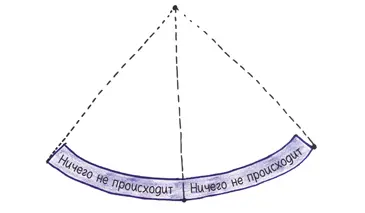
Посмотрите на центральную часть балки. На полпути между сжатием наверху и растяжением внизу средняя часть балки не испытывает абсолютно никакого напряжения. Ее изгиб — беззаботная улыбка пацана, который игнорирует ваш призыв о помощи. Материал средней части балки растрачен впустую, это не лучше, чем бесполезная масса пирамиды. Обычная балка действует вполсилы, как ленивый школьник, который напрягается на 50 %.

Любой учитель знает, какая фраза здесь должна последовать: «Так никуда не годится». В архитектуре каждая унция имеет значение, строите ли вы башню, щекочущую небеса, мост через каньон или захватывающие дух американские горки.

Будьте уверены: архитекторы не дураки {21} 21 Тед Мосби не в счет. (Тед Мосби — нелепый архитектор, главный персонаж комедийного сериала «Как я встретил вашу маму». — Прим. пер. ) . У них есть план.

Я сказал, что архитекторы не дураки? Возможно, мне придется взять свои слова обратно, когда вы услышите, как они решили эту проблему. Из-за того, что верхняя и нижняя части балки принимают на себя все напряжение, пока средняя часть паразитирует на их усилиях, блестящее решение, найденное архитекторами, состояло в том, чтобы изготавливать балки без средних частей .

Не стоит восклицать; я все прекрасно понимаю. Балка без средней части представляет собой две отдельные балки, и это так себе решение.

Если только не… вырезать небольшую часть из середины балки. Вы оставляете бóльшую часть материала по краям и тонкий соединительный слой посредине [36] Я снова позаимствовал эту информацию у Сальвадори. Как отмечает Уилл Уонг, в более традиционном представлении на первый план в этом случае выходят нужные нам свойства (распределение напряжение, предотвращение крутящего момента и т. д.), обусловленные тем, что поперечное сечение балки имеет форму буквы I. . В результате поперечное сечение балки напоминает латинскую букву I («Ай»); поэтому она называется Ай-балка {22} 22 В русском языке используется термин «двутавровая балка» (от лат. taurus — бык), потому что она «рогатая» с обеих сторон. — Прим. пер. .

Хорошее начало. Но у нас все еще остается потраченный впустую материал в центре. Поэтому мы запускаем вторую фазу плана архитекторов: просверливаем отверстия в центральной части балки.

Каждое отверстие экономит драгоценные ресурсы, при этом мы почти ничего не теряем в прочности. Чем больше отверстий, тем больше материала мы экономим, и это означает, что лучше всего изрешетить центральную часть балки — оставить как можно меньше материала и сделать как можно больше пустот.

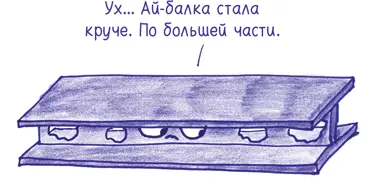
Но погодите. Перед тем как начать волей-неволей просверливать эти отверстия, нам нужно разработать план. Какое распределение отверстий минимизирует расход материала и при этом сохранит прочность и жесткость конструкции? Где бы нам найти простую и упругую форму, не говоря уже о том, чтобы она хорошо подходила для плоской, почти двумерной области в центре Ай-балки?

Есть всего одна фигура, способная ответить на этот вызов. Слабовольный квадрат не подходит: его углы покосятся. Трусливый пятиугольник разрушится под давлением. И забудьте про бесхребетного перебежчика, известного под именем шестиугольник. Лишь супермен среди многоугольников может выдержать напряжение и стоически, непреклонно сохранить свою форму.

Позовите к телефону Треугольник.

Соединяя треугольники в единую конструкцию, вы создаете ферму {23} 23 От лат. firmus — прочный. Сельское хозяйство ни при чем. — Прим. пер. . В ферменной конструкции каждый элемент подвергается растяжению или сжатию. Фермы позволяют не тратить материал впустую — так охотники до упора разделывают тушу животного.

В Древнем Египте треугольник делал свое дело на пустырях, позволяя землемерам проделывать ловкие фокусы, пока софиты светят на других героев. Затем, спустя тысячелетия, по ту сторону океана, треугольники переместились из-за кулис на авансцену.

В XIX и начале XX века обитатели Северной Америки освоили пустой континент. Поскольку он был довольно бугристым, требовались мосты всех видов, от скромных пешеходных до гигантских железнодорожных. Для этих мостов потребовались ферменные конструкции. А что нужно для ферменных конструкций? Треугольники, естественно.

Ферменная конструкция Пратта [37] Мои познания о ферменных конструкциях почерпнуты из величайшего человеческого творения — «Википедии». Подробности на страницах https://en.wikipedia.org/wiki/Truss и https://en.wikipedia.org/wiki/Truss_bridge . , разработанная двумя братьями в 1844 году, состоит из рядов прямоугольных треугольников. Она покорила Соединенные Штаты, оставаясь популярной на протяжении десятилетий.