Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

У этого правила есть компаньон, даже глубже и могущественнее него: « Если три отрезка все-таки образуют треугольник, то один и только один ». Поскольку даны три отрезка, импровизации и выдумки здесь неуместны. Есть всего один шаблон.

Например, договоримся, что длины сторон будут равны конкретным величинам (скажем, 5, 6 и 7 cм), разойдемся по отдельным комнатам и сконструируем наши персональные треугольники. Даю гарантию, что мы выйдем оттуда с одинаковыми изделиями.

Поглядите: я кладу мою самую длинную рейку на пол, приставляю и скрепляю две других. Готово! Скосите угол влево, и одна сторона выскользнет; скосите вправо — выскользнет другая. Математики называют такое решение единственным . Даже не предвосхищая ваш метод, я знаю, что вы придете к тому же решению, так как иных решений нет.

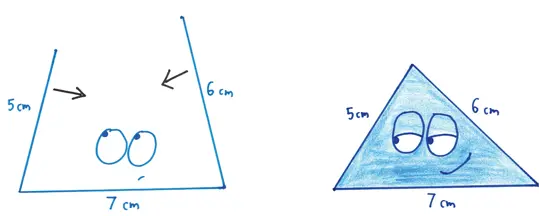
Эта истина верна лишь для треугольников. Ни один другой многоугольник на нее не притязает.

Попробуйте проделать то же самое с четырехугольником — кузеном треугольника. Одну рейку я кладу на пол. Следующие две устанавливаю вертикально. И водружаю последнюю рейку сверху, для надежности склеивая концы скотчем. Однако начинает задувать ветерок. Мой квадрат косится. Вся конструкция кренится вправо, как складной стул. Каждую секунду возникает новая фигура, от «квадрата» и «почти квадрата» до «чего-то вроде ромба» и «тощего сверхзаостренного ромба».

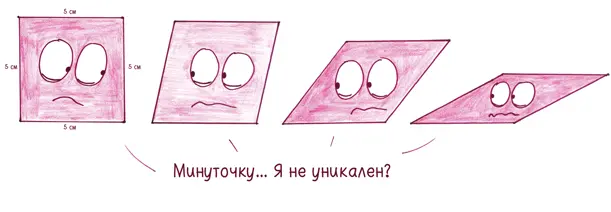
Четыре стороны с конкретными длинами не задают единственную фигуру. Наоборот, они задают бесконечное семейство возможных фигур. Любую из них можно превратить в другую, приложив небольшое усилие.

Итак, мы наблюдаем скрытое волшебство треугольника, его секретную идентичность: не просто трехсторонность, а жесткость, которую она за собой влечет.

Вязальщики египетских узлов знали это превосходство. Натягивая канат с 12 узлами, они вызывали из небытия пифагоров треугольник, выколдовывали из каната прямой угол. Вместо этого можете сделать из каната квадрат, но будьте аккуратны: на ваш клич отзовется целое семейство нежелательных фигур. Даже если натянуть канат потуже, углы четырехугольника не удастся удерживать без сбоев. То же самое верно для пятиугольников, шестиугольников, семиугольников и прочих родичей из семейства многоугольников. Никто не в силах сделать то, что может треугольник.

Пирамиды, будучи объемными фигурами, не обладают этим сильным преимуществом {20} 20 Смотря какие пирамиды. Треугольная пирамида (это тетраэдр, если все ребра равны, как у старого молочного пакета) — жесткая фигура, так что дело не в объемности. — Прим. науч. ред. . Кубы, конусы, усеченные пирамиды [32] Усеченная пирамида — многогранник с двумя параллельными основаниями и гранями-трапециями. По-английски она называется frustum — это слово стоит знать. — все они сгодятся для выполнения воли фараона. Шершавому языку камня все равно, какую выговаривать фигуру.

Нет-нет, в мои намерения не входило унижать пирамиды. Да и попробуйте унизить кирпичную махину в девять миллионов тонн. Я восхищен космической точностью этих кирпичей: длины сторон составляют около 20 см, края ориентированы по сторонам света с погрешностью менее 0,1°, углы отличаются от прямого менее чем на 0,01°. Да, египетские котики хорошо знали математику.

Но я должен подчеркнуть, что это триумф землемеров, а не инженеров. Великая пирамида остается, по сути дела, нагромождением блоков. Это круто, если вы хотите воздвигнуть монумент фараонову бессмертию, но использовать такое здание в практических целях, знаете ли, не прикольно. Незатейливые камеры и тесные туннели пирамиды составляют менее 0,1 % ее объема. Вообразите сплошной стальной брусок размером с Эмпайр-стейт-билдинг с одним-единственным щелевидным этажом высотой 60 см, и вы тоже начнете стремиться к более эффективному строительному плану [33] «Википедия» указывает размеры трех туннелей (нисходящего, восходящего и горизонтального) и трех камер (Царская палата, Царицына палата, большая галерея). Их суммарный объем составляет около 1340 м 3 , т. е. примерно 0,05 % от объема пирамиды 2 600 000 м 3 . Я округлил это число до 0,1 %, затем (снова низкий поклон «Википедии») вычислил объем Эмпайр-стейт-билдинг (2 800 000 м 3 ), и 0,1 % от этого числа составляет 2800 м 3 . Разделив объем на площадь одного этажа (около 7400 м 2 ), вы получите высоту 38 см. Но едва я закончил рукопись книги, в пирамиде была обнаружена потайная камера! Я округлил до двух футов (около 60 см), и мое округление покрывало эту неучтенную ошибку. .

В последующие века архитекторы будут искать новые поэтические структуры. Они будут строить мосты шире неба и башни выше Вавилонской. И для этого им понадобится фигура необычайной стойкости, обладатель единственного в своем роде непреклонного характера — треугольный, трехсторонний герой.

А теперь наша история пересекается с другой — сагой о человеческой архитектуре, охватывающей 10 000 лет. Краткое содержание предыдущих серий:

1. «Снаружи» — плохое место для жизни. Может похолодать, негде хранить ваши вещи, иногда появляются медведи. Поэтому люди изобрели «внутри».

2. Чтобы создать «внутри», сделайте большую полую конструкцию и поселитесь там.

3. Если ваша конструкция уютна и сделана из подходящего материала, то жить внутри будет приятно и она не рухнет вам на голову. Это и называется «архитектура».

Окей, теперь, когда мы вошли в курс дела, я могу представить вам важного вспомогательного персонажа [34] Каламбур, сознательный на 100 %. в истории треугольника — балку. Если вы архитектор, стремящийся избежать (А) пирамидальных монолитов и (Б) обваливающихся потолков, то балки, скорее всего, станут важным фактором в процессе создания ваших конструкций.

Полезное действие балки заключается в том, что она превращает вертикальные силы в горизонтальные [35] Я умыкнул эти сведения из книги Сальвадори (Why Buildings Stand Up) и, вне всяких сомнений, что-нибудь упустил в пересказе. . Например, представьте себе доску, перекинутую через ров. Когда вы встанете на эту доску, ваш вес потянет ее вниз. Но настоящая опора не внизу — она на концах доски, где та упирается в землю. Сила, приложенная в центре, распределяется вдоль доски.