Бен Орлин - Математика с дурацкими рисунками. Идеи, которые формируют нашу реальность

С какой стати? Но ведь у формы два измерения: длина и ширина. Удваивая длину, мы удваиваем площадь формы. Удваивая ширину, мы снова удваиваем площадь. Таким образом, площадь удваивается дважды. Иными словами, умножается на 4.

Так происходит всякий раз, когда вы увеличиваете прямоугольник. Утраиваете стороны? Площадь возрастает в девять раз. Упятеряете стороны? Площадь возрастает в 25 раз. Умножаете стороны на девять тыщмиллионов? Площадь увеличивается в 81 тыщмиллионов тыщмиллионов раз.

Или, говоря точнее: увеличивая стороны в r раз, вы увеличиваете площадь в r2 раз.

Так происходит не только с прямоугольниками. Тот же принцип работает для всех двумерных фигур: трапеций, треугольников, кругов и других емкостей, в которые вы укладываете заветное шоколадное тесто. Когда стороны увеличиваются, площадь увеличивается существенно больше.

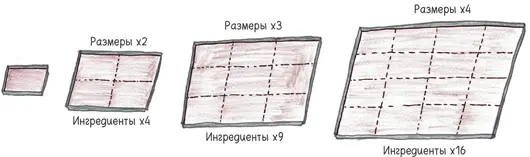
Вернемся на кухню. Мы уже смешали вчетверо большее количество ингредиентов, когда на дальней полке обнаруживаются формы, которые мы искали все это время. Мы осыпаем друг друга упреками, но потом смеемся: кому охота пререкаться, когда скоро будет готово шоколадное великолепие?

Теперь перед нами встает выбор: готовить торт в одной большой форме или в четырех поменьше?

Это басня, поэтому мы пренебрегаем деталями. Забудьте о температуре, времени приготовления, теплопередаче и предстоящем мытье посуды. Сосредоточьтесь на одном параметре: размерах форм для выпечки.

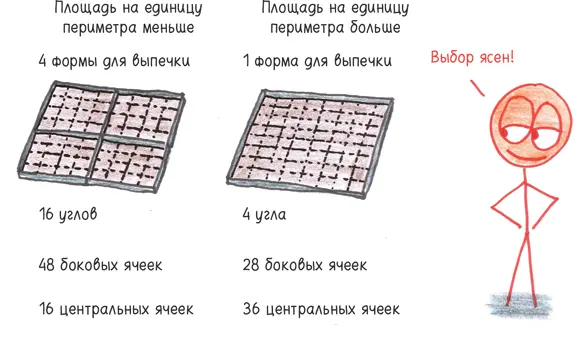
Если форма для тортов стала больше, ее периметр (одномерная величина) увеличился. Но ее площадь (двумерная величина) увеличилась еще больше. Это означает, что у четырех форм поменьше общий периметр будет больше, хотя их площадь равна площади большой формы.

У маленьких форм на единицу периметра приходится меньше площади, а у большой формы — больше.

Как я ни пытаюсь, я не могу представить себе людей, которые любят обгорелые боковушки торта. Кто променяет шоколадное чудо на пытку для зубов, хрустящее недоразумение? Мне легче представить, что они предпочитают кости вместо мяса, сухари вместо крекеров, побочные эффекты вместо обезболивающего. Этим людям нет ни объяснения, ни оправдания. Берите большую форму или расходитесь по домам.

Около 2300 лет назад жители греческого острова Родос отразили нападение Александра Македонского {24} 24 Плиний Старший пишет, что Колосс Родосский был построен после победы над Деметрием I Македонским, внучатым племянником Александра Великого (см. «Естественная история», XXXIV, 41). — Прим. пер. . В порыве самовосхваления они поручили местному скульптору Харесу построить грандиозную триумфальную статую [44] Я узнал эту историю из книги Kitty Ferguson, Pythagoras: His Lives and the Legacy of a Rational Universe (London: Icon Books, 2010). Как и многие басни, она, скорее всего, носит апокрифический характер. . По легенде, вначале Харес планировал построить 15-метровую бронзовую скульптуру.

— А не сделать ли нам статую побольше? — сказали родосцы. — Знаешь что — удвоим высоту! Сколько это будет стоить?

— В два раза дороже, конечно, — сказал Харес.

— По рукам! — сказали родосцы.

В ходе строительства Харес увидел, что его средства иссякают. Материальные издержки ошеломили его; они намного превышали отпущенный бюджет. Впереди маячило банкротство. Говорят, что Харес расстался с жизнью, чтобы избежать финансового краха, и не увидел, как был завершен его шедевр. Но, возможно, перед тем как умереть, он осознал свою ошибку.

Он постеснялся взвинтить цену.

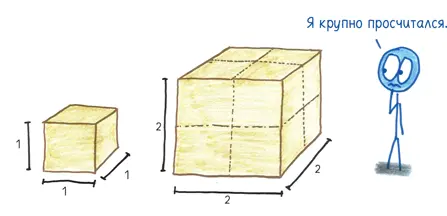
Для того чтобы понять, почему это так, забудьте все детали. Не обращайте внимания на рынок труда для греческих строителей или оптовые цены на бронзу. Черт возьми, забудьте даже об искусстве: представьте, что Харес просто строит исполинский бронзовый куб. Мы должны сосредоточиться на одном всепоглощающем вопросе: на размерах.

Что происходит, когда вы удваиваете размеры трехмерной геометрической фигуры?

Хорошо, вы удвоили длину; объем вырос в два раза. Вы удвоили ширину, и объем снова вырос в два раза. И вы удвоили высоту, удвоив объем в третий раз. Это тройной дубль, хотя не такой, как у Рассела Уэстбрука {25} 25 Американский баскетболист. — Прим. пер. : в данном случае тройное удвоение означает умножение на 8.

Результат настолько же ясен, насколько поразителен: объем растет с огромной скоростью.

Утраиваем стороны куба? Объем вырастает в 27 раз. Умножаем стороны на 10? Объем абсурдным образом увеличивается в 1000 раз . И то, что верно для кубов, верно для всех трехмерных геометрических фигур: пирамид, шаров, призм и (к несчастью для Хареса) роскошных статуй бога солнца Гелиоса. В точных терминах: умножьте длины сторон на r , и объем вырастет в r3 раз.

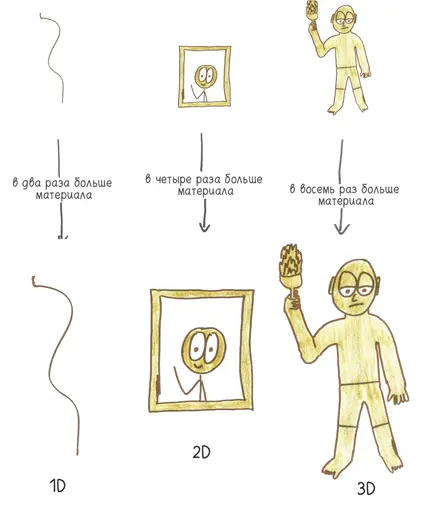
Если бы Харес создавал одномерное произведение искусства (Колоссальную Родосскую Струну) , эстетика, возможно, пострадала бы, но его ценовая политика отлично бы сработала: удваивая длину, необходимо взять в два раза больше бронзы. Или, предположим, ему было бы поручено создать двумерную картину (Колоссальный Родосский Портрет) . Цена по-прежнему осталась бы заниженной, но все же не настолько: удваивая стороны холста, мы учетверяем его площадь, поэтому требуется в четыре раза больше краски. Увы, Харес имел несчастье работать во всех трех измерениях. Удвоение высоты статуи означало, что понадобится в восемь раз больше бронзы.

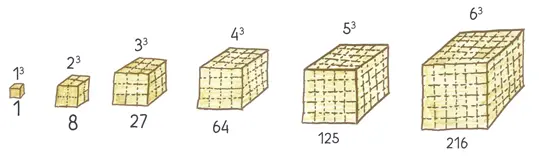
Когда длины сторон растут, площадь растет гораздо быстрее, а объем — еще быстрее. Колосс Родосский — одно из чудес древнего мира — обрек своего творца на муки по той простой причине, что был трехмерным [45] Джон Коуэн (я благодарю его за сверку фактов в этой главе и за то, что он никогда не кичится и не подавляет своей эрудированностью) добавил один штрих: «На самом деле Колосс Родосский, как и статуя Свободы, был полым: бронзовые пластины и железные арматурные прутья. Следовательно, при увеличении высоты в n раз цена вырастала всего лишь в n 2 раз». Все равно чересчур для бедняги Хареса. .