Жюль Пуанкаре - Теорема века. Мир с точки зрения математики

Назовем индуктивным числом всякое число, которое составляет часть всех рекуррентных классов.

При каком условии это последнее определение, играющее существенную роль в доказательстве Уайтхеда, будет «предикативным» и, следовательно, приемлемым?

Согласно предшествующему изложению под всеми рекуррентными классами надо понимать все классы, в определение которых не входит понятие об индуктивном числе.

Без этого можно впасть в ложный круг, который и породил антиномии.

Но Уайтхед не принял этой предосторожности.

Его рассуждение ложно; именно оно и повело к антиномиям; оно было незаконным, когда давало ложные результаты, и остается незаконным, когда приводит случайно к правильному результату.

Определение, которое содержит заколдованный круг, ничего не определяет. Не к чему говорить: мы уверены, что, какой бы смысл ни был дан нашему определению, все же существует по крайней мере нуль, который принадлежит классу индуктивных чисел. Дело не в том, чтобы узнать, пуст ли этот класс, а в том, чтобы его строго отграничить. «Непредикативный» класс – это не пустой класс, а класс, в котором граница оказывается неопределенной.

Излишне прибавлять, что это частное возражение оставляет в силе те общие возражения, которые приложимы ко всем доказательствам.

Второй гласит:

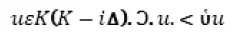
Первый постулат не более очевиден, чем принцип, подлежащий доказательству. Второй не только не очевиден, но и ложен, как это показал Уайтхед и как это, впрочем, заметил бы любой лицеист математического класса, если бы аксиома была выражена на понятном языке. Ибо эта аксиома означает: число комбинаций, которые можно образовать из нескольких предметов, менее числа этих предметов.

В известном доказательстве Цермело опирается на следующую аксиому:

В какой-либо совокупности (или даже в каждой из совокупностей некоторой совокупности совокупностей) мы можем всегда выбрать наудачу один элемент (даже тогда, когда эта совокупность совокупностей обнимает бесконечно много совокупностей). Тысячу раз применяли эту аксиому, не высказывая ее. Но лишь только она была высказана, как появились сомнения. Одни математики, как Борель, ее отвергают, другие восхищаются ею. Посмотрим, что об этом думает Рассел в своей последней статье.

Он не высказывается, но те размышления, которым он предается, очень знаменательны.

Однако сначала один наглядный пример. Допустим, что мы имеем столько пар сапог, сколько есть целых чисел, так что мы можем нумеровать пары от 1 до бесконечности. Сколько мы будем иметь сапог? Будет ли число сапог равно числу пар? Да, если в каждой паре правый сапог отличается от левого, ибо в таком случае достаточно будет обозначить номером 2 n − 1 правый сапог n -й пары, а номером 2 n – левый сапог n -й пары. Нет, если правый сапог подобен левому, так как в этом случае такая операция будет невозможна. Иначе придется допустить аксиому Цермело, потому что тогда можно в каждой паре выбрать наудачу сапог, который будет рассматриваться как правый.

Доказательство, действительно основанное па принципах аналитической логики, будет составляться из ряда предложений. Одни из них, которые служат посылками, будут тождествами или определениями; другие будут последовательно выведены из первых. Но, хотя связь между каждым предложением и последующим замечается непосредственно, трудно будет с первого взгляда увидеть, как мог совершиться переход от первого предложения к последнему, и явится соблазн рассматривать это последнее как новую истину. Но если последовательно заменить фигурирующие в нем различные выражения их определениями, если провести эту операцию насколько можно далеко, то в итоге останутся только тождества, так что все сведется к бесконечной тавтологии. Логика, следовательно, окажется бесплодной, если не будет оплодотворена интуицией.

Вот что я уже писал давно. Логистики исповедуют противоположную точку зрения и думают, что доказали ее, показав действительно новые истины. Но каким образом?

Почему, применяя к их рассуждениям описанный только что прием, т. е. заменяя определенные термины их определениями, мы не видим, чтобы они сливались в тождества, как это бывает с обыкновенными рассуждениями? Значит, этот прием к ним неприменим. А почему? Потому что их определения непредикативные и дают тот заколдованный круг, который я отметил выше; непредикативные определения не могут стать на место определяемого термина. В этих условиях логистика является уже не бесплодной, она родит антиномию.

Вера в существование актуальной бесконечности дала начало этим непредикативным определениям. Я объяснюсь. В этих определениях фигурирует слово «все», как это видно из приведенных выше примеров. Слово «все» имеет достаточно точный смысл, когда речь идет о бесконечном [28] В оригинале опечатка, следует читать «конечном». – Прим. ред . числе предметов; для того чтобы оно имело также смысл, когда предметов имеется бесчисленное множество, необходимо, чтобы существовало актуально бесконечное. В противном случае на все эти предметы нельзя было бы смотреть как на данные до их определения; вместе с тем определение понятия N , если оно зависит от всех предметов A , может страдать пороком заколдованного круга, раз между предметами А имеются такие, которые нельзя определить без помощи самого понятия N .

Правила формальной логики выражают просто свойства всех возможных классификаций. Но для того чтобы эти правила были приложимы, необходимо, чтобы классификации оставались неизменными, чтобы их не приходилось изменять на протяжении рассуждений. Если приходится распределять конечное число предметов, то легко сохранить эти классификации без изменения. Если же предметы имеются в неопределенном количестве, т. е. если имеется возможность постоянного и внезапного появления новых предметов, то может случиться, что такое появление обяжет к изменению классификации. Отсюда опасность антиномий.

Нет актуальной бесконечности. Канторианцы забыли это и впали в противоречие. Верно то, что теория Кантора оказала услуги, но это было тогда, когда она применялась к истинной проблеме, термины которой были отчетливо определены; тогда можно было подвигаться вперед без опасений.

И логистики, подобно канторианцам, забыли об этом и встретились с теми же затруднениями. Но нужно знать, попали ли они на этот путь случайно или по необходимости.

Для меня вопрос не представляет сомнений. Вера в актуально бесконечное является существенной в логике Рассела. Этим она отличается от логистики Гильберта. Гильберт становится на точку зрения объема именно для того, чтобы избежать канторовских антиномий; Рассел становится на точку зрения содержания. Для него, следовательно, род предшествует виду и summum genus [29] Первый, главный род ( лат .). – Прим. ред . предшествует всему. Это не представляло бы неудобства, если бы summum genus был конечным; но если он бесконечен, то приходится бесконечное ставить перед конечным, т. е. рассматривать бесконечное как актуальное.