Дмитрий Паршаков - Алгоритм решения 10 проблемы Гильберта

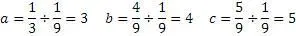
И вновь получилась уже известная тройка 3,4,5.

На основании полученных результатов, можно записать алгоритм кратности

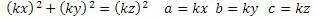
Осталось объединить получившиеся алгоритмы в один универсальный.

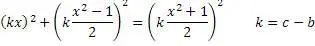
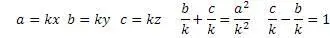
Теперь можно вычислять абсолютно все пифагоровы тройки, зная или задавая значение любого одного числа из тройки и задавая кратность уравнению.

Задача № 1

Найти значения чисел «а» и «b» в уравнении

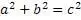
Условия задачи

Дано:

Значение числа «с»=161

Коэффициент кратности уравнения «k»=7

Воспользуемся формулами универсального алгоритма

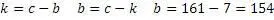
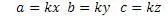
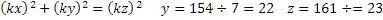
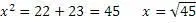
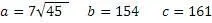
Проверим получившийся результат

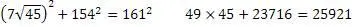
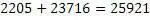
Задача решена, числа найдены.

Задача № 2

Требуется найти натуральные значения чисел «b» и «с» для уравнения

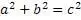
Условия задачи

Дано: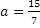

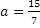
Воспользуемся формулами, для нахождения исходных «троек»

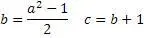
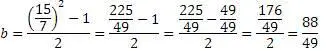
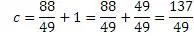
Подставим числа в формулу

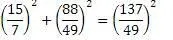
Теперь нужно привести все числа к общему знаменателю

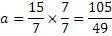
Остается воспользоваться формулой кратности 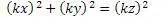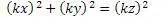и разделить числа на коэффициент кратности,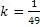

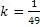
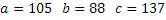
Проверяем

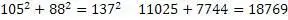
Задача решена, числа найдены.

Из этой задачи видно, что знаменатель нужно помножить на числитель. Поэтому можно создать следующий алгоритм для произвольных «k» и «а».

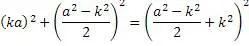
Проверим действие этого алгоритма

Пример № 7

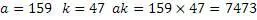
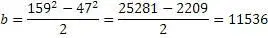
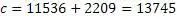
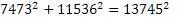
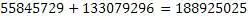
Алгоритм работает. Для генерации пифагоровых троек можно использовать как универсальный алгоритм, так упрошенный.

Для чисел кратным 4-ем существует еще один алгоритм. Его можно использовать для упрощенного нахождения пифагоровых троек.

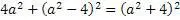
Пример № 8

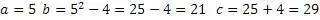
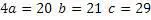
Получилась уже известная тройка.

Постановка вопроса о разрешимости диофантовых уравнений подразумевала также доказательство теоремы Ферма[5]. Почему же не может существовать целочисленные значения для уравнений вида

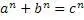
При

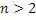
Собственно от формулы Пифагора это уравнение отличается только значением степени, поэтому формула Пифагора принадлежит к этим уравнениям.

А раз она принадлежит к данным уравнениям, то для нахождения решений можно применить универсальный алгоритм. Для этого нужно это произвольное уравнение перевести в степень 2

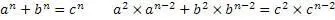
Упростим уравнение

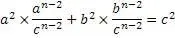
Теперь можно применить одну из формул алгоритма

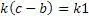
Для нахождения значений этого уравнения, кратностью можно пренебречь, так как в любом случае существует исходная тройка взаимно простых чисел. Поэтому применим формулу исходного алгоритма

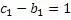
По условиям алгоритма, должно получиться равенство

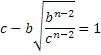
Предположим, что такое равенство возможно. Но коэффициент числа «b» меньше 1, так как сумма, которую представляет число «с», больше слагаемого, которое представляет число «b».