Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

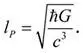
Если подставить измеренные значения ħ, G и c , то планковская длина оказывается равной около 10 –35 метра – ошеломительно малое расстояние, которое примерно в сто миллионов триллионов раз меньше диаметра протона. Соответствующее планковское время – это время, за которое свет проходит такое расстояние, и оно приблизительно равно 10 –43 секунды. При меньших величинах пространство и время теряют смысл.

Эти числа ограничивают наши возможности деления пространства и времени. Чтобы ощутить уровень точности, о котором мы говорим, посмотрим, сколько цифр нам понадобится для проведения одного из самых экстремальных сравнений. Возьмем самое большое возможное расстояние – оцениваемый диаметр Вселенной, и разделим его на самое маленькое возможное расстояние – планковскую длину. Это невообразимо огромное отношение расстояний выражается числом, состоящим всего лишь из шестидесяти цифр. Хочу подчеркнуть – всего шестидесяти. И это самое большое число, которое понадобится, чтобы выразить одно расстояние через другое. Использование большего количества – скажем, сотни цифр, не говоря уже о еще б о льших числах – было бы колоссальным излишеством, не требующимся для описания каких-либо реальных расстояний в материальном мире [42].

И все же в анализе мы постоянно используем бесконечно много цифр. Уже в школе учеников просят думать о числах наподобие 0,333…, причем десятичное разложение продолжается бесконечно. Мы называем эти числа действительными, хотя в них нет ничего действительного. Определение такого числа с помощью бесконечного количества знаков после запятой не имеет ничего общего с реальностью, по крайней мере в том ее понимании, которое бытует в современной физике.

Но если действительные числа недействительны, то почему математики так их любят? И почему школьники вынуждены их изучать? Потому что они нужны в анализе. С самого начала анализ упорно настаивал, что все – пространство и время, вещество и энергия, все объекты, которые когда-либо были или будут, – должно считаться непрерывным. Соответственно, все это можно и нужно выражать действительными числами. В этом идеализированном воображаемом мире мы делаем вид, что все можно без конца делить на все более мелкие кусочки. На этом предположении построена вся теория анализа. Без него нельзя вычислить пределы, а без пределов анализ бы остановился. Если бы мы использовали только десятичные дроби с не больше чем 60 цифрами после запятой, то числовая прямая была бы испещрена дырками. Дыры были бы на месте числа π, квадратного корня из 2 и многих других чисел, для выражения которых требуется бесконечное число цифр после запятой. Отсутствовала бы даже такая простая дробь, как 1/3, потому что для выражения ее местоположения на цифровой прямой тоже требуется бесконечное число цифр (0,333…). Если мы хотим думать о всей совокупности чисел, образующих прямую, эти числа тоже должны быть действительными. Возможно, они только приближение к реальности, но они изумительно работают. Как и везде в анализе, бесконечность все упрощает и в случае бесконечных десятичных знаков после запятой.

Примерно через двести лет после того, как Зенон задумался о природе пространства, времени, движения и бесконечности, еще один мыслитель счел бесконечность неотразимой. Его звали Архимед [43]. Мы уже встречались с ним, когда говорили о площади круга, но он легендарен и по многим другим причинам.

Начнем с того, что о нем ходит много забавных историй [44]. В некоторых он предстает этаким чудаком-математиком. Например, историк Плутарх рассказывает [45], что Архимед настолько увлекался геометрией, что «забывал о пище и уходе за телом» [46], [47]. (Это определенно верно. Для многих из нас, математиков, еда и личная гигиена не входят в список приоритетов.) Из-за этого, как говорит Плутарх, ученого даже насильно заставляли принимать ванну [48]. Забавно, что он занимался этим с такой неохотой, учитывая, что именно с купанием связана история, которую знают все. По словам римского архитектора Витрувия [49], Архимед был настолько возбужден внезапным озарением во время купания, что выскочил из ванны и побежал голышом по улице, крича: «Эврика!» («Нашел!»).

Другие истории рисуют его магом военного искусства, воином-ученым – настоящим отрядом смерти из одного человека. Согласно этим легендам, когда его родной город Сиракузы в 212 году до нашей эры осадили римляне, Архимед – к тому времени уже почти 70-летний старик – помогал защищать город, применяя свои знания о рычагах и блоках для создания фантастического оружия – «боевых машин», таких как крюки и гигантские краны, которые поднимали римские корабли из воды и стряхивали с них моряков, как вытряхивают песок из обуви. Плутарх описывал эту ужасающую сцену так: «Нередко взору открывалось ужасное зрелище: поднятый высоко над морем корабль раскачивался в разные стороны до тех пор, пока все до последнего человека не оказывались сброшенными за борт или разнесенными в клочья, а опустевшее судно разбивалось о стену или снова падало на воду, когда железные челюсти разжимались» [50], [51].

Если говорить о более серьезных вещах, то все школьники и инженеры помнят закон Архимеда (на тело, погруженное в жидкость, действует выталкивающая сила, равная весу вытесненной жидкости) и закон рычага (предметы на противоположных плечах рычага уравновешиваются, если их массы обратно пропорциональны расстояниям от точки опоры). Обе идеи имеют бесчисленные практические приложения. Закон Архимеда объясняет, почему одни объекты плавают, а другие – нет. Он также лежит в основе теории кораблестроения, теории остойчивости судов и проектирования морских нефтебуровых платформ. А принцип рычага вы, сами того не сознавая, применяете каждый раз, когда используете ножницы для ногтей или лом.

Возможно, Архимед был потрясающим конструктором боевых машин и, несомненно, блестящим ученым и инженером, но по-настоящему в пантеон великих его вводят достижения в математике. Он проложил путь к интегральному исчислению. Глубочайшие идеи, содержащиеся в его работах, больше не встречались почти два тысячелетия. Сказать, что он опередил свое время, – значит ничего не сказать. Кто-нибудь опережал свое время настолько ?

В работах ученого постоянно появляются две стратегии. Первая – активное использование принципа бесконечности. Чтобы изучать загадки кругов, сфер и прочих криволинейных форм, Архимед всегда аппроксимировал их с помощью прямолинейных форм, состоящих из прямых и кусков плоскостей, похожих на грани драгоценных камней. Воображая все большее количество частей и делая их все меньше по размеру, он подгонял свои приближения все ближе к истине, подходя к пределу с бесконечным количеством частей. Такая стратегия требовала филигранного обращения с суммами и головоломками, поскольку для получения своих выводов ему приходилось складывать множество чисел и частей.