Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Вторая примечательная стратегия – сочетание математики с физикой, идеального с реальным. В частности, он объединял геометрию, науку о формах, с механикой, изучающей движение и силы. Иногда он использовал геометрию, чтобы пролить свет на механику; иногда ход мыслей бывал обратным – механические соображения рождали идеи для чистых форм. Искусно используя обе стратегии, Архимед смог глубоко проникнуть в тайну кривых.

Когда я иду на работу или гуляю вечером с собакой, шагомер в моем iPhone отслеживает пройденное расстояние. Вычисления просты: приложение оценивает длину шага, исходя из моего роста, считает количество сделанных шагов, а затем перемножает эти два числа. Пройденное расстояние равно длине шага, умноженной на количество шагов.

Архимед использовал аналогичную идею для вычисления длины окружности и оценки числа π [52]. Представьте, что окружность – это дорожка для ходьбы. Путь будет выглядеть примерно так:

Каждый шаг представлен коротким отрезком. Умножив число шагов на длину одного отрезка, мы можем оценить длину пути. Конечно, это всего лишь оценка, потому что окружность на самом деле состоит не из прямых отрезков, а из дуг. Заменяя каждую дугу отрезком, мы слегка сокращаем путь. Поэтому такое приближение занижает реальную длину круговой дорожки. Но, по крайней мере теоретически, сделав достаточно большое количество достаточно маленьких шагов, мы можем приблизить длину дорожки с желаемой точностью.

Архимед проделал ряд подобных вычислений, начав с пути из шести шагов, то есть с правильного шестиугольника [53].

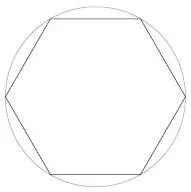
Это был удобный базовый лагерь перед штурмом более сложных вычислений. Преимущество шестиугольника в том, что его периметр – сумму длин всех шести сторон – вычислить очень просто. Он в шесть раз больше радиуса круга. Почему? Потому что шестиугольник состоит из шести равносторонних треугольников, длина сторон которых равна радиусу круга.

Шесть сторон таких треугольников образуют периметр шестиугольника.

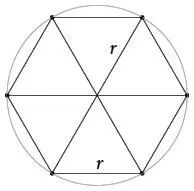
Получается, периметр в шесть раз больше радиуса, то есть p = 6 r . Тогда, поскольку длина окружности C больше, чем периметр шестиугольника p , должно выполняться C > 6 r .

Это рассуждение дало Архимеду нижнюю границу для числа, которое мы называем пи , обозначаем греческой буквой π и определяем как отношение длины окружности к ее диаметру. Так как диаметр d равен 2 r , то из неравенства C > 6 r следует:

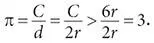
Таким образом, с помощью шестиугольника можно определить, что π > 3.

Конечно, шесть – это смехотворно малое число шагов, и получившийся шестиугольник – очень грубая карикатура на окружность, но для Архимеда он был всего лишь началом. Выяснив все, что мог дать ему шестиугольник, он уменьшил длину шагов, но увеличил их количество. Он добавил средние точки всех дуг и вместо одного шага стал делать два.

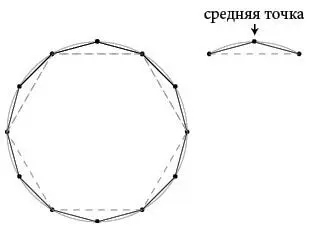
Он, как одержимый, продолжал делать так снова и снова, перейдя от шести шагов к 12, потом к 24, 48 и 96, вычисляя периметр получающихся многоугольников с точностью, вызывающей мигрень.

К сожалению, по мере уменьшения длины отрезков стало все труднее вычислять их длину, поскольку ему приходилось постоянно применять теорему Пифагора, а для этого требовалось находить квадратные корни – чертовски сложная вещь, когда приходится считать вручную. Кроме того, чтобы получить не только оценку снизу, но и сверху, Архимед использовал второй многоугольник – описанный вокруг окружности; его периметр был больше, чем длина окружности.

Я хочу сказать, что вычисление Архимедом числа π было героическим подвигом – и с логической, и с арифметической точки зрения. В итоге, использовав 96-угольник, вписанный в круг, и 96-угольник, описанный около круга, он доказал, что число π больше, чем 3 + 10/71, и меньше, чем 3 + 10/70.

Забудьте на минуту о математике. Просто насладитесь этим результатом на визуальном уровне:

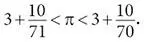
Неизвестное и вечно непостижимое число π оказалось зажато в тиски между двумя почти одинаковыми числами, отличающимися только знаменателями 70 и 71. Одно из полученных граничных значений – число 3 + 10/70 = 22/7 – стало знаменитым приближением для π, знакомым всем школьникам; к сожалению, многие ошибочно считают его самим числом π.

Метод, который использовал Архимед (он основывается на более ранних работах греческого математика Евдокса), сегодня известен как метод исчерпывания, когда неизвестное число π оказывается зажатым между двумя известными числами. С каждым удвоением границы сближаются, оставляя числу π все меньше места.

Окружности – это простейшие кривые в геометрии. Тем удивительнее, что определение их количественных характеристик выходит за ее рамки. Например, вы не найдете упоминания о числе π в «Началах» Евклида, написанных за одно-два поколения до Архимеда. Вы найдете там доказательство (методом исчерпывания), что отношение площади круга к квадрату его радиуса одинаково для всех кругов, но ни малейшего намека на то, что это универсальное число близко к 3,14. Такое упущение Евклида было сигналом, что тут нужно что-то более глубокое. Чтобы разобраться с числовым значением π, потребовалась новая математика, которая бы могла работать с криволинейными формами. Как измерить длину кривой, площадь криволинейной фигуры или объем криволинейного тела? Эти актуальные вопросы увлекли Архимеда и позволили сделать первые шаги по направлению к тому, что мы сейчас именуем интегральным исчислением. Число π было его первым триумфом.

Современным умам может показаться странным, что число π не появляется в формуле Архимеда для площади круга, A = rC / 2 и что он никогда не записывал уравнения типа C = π d для выражения длины окружности через диаметр. Он избегал это делать, поскольку π не было для него числом. Это было просто отношение двух длин, длины окружности и ее диаметра. Это была какая-то величина, а не число.