Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Когда я читаю, как Архимед радуется обнаружению соотношений для площади поверхности и объема шара, я испытываю аналогичные ощущения. Или, скорее, понимаю, что он чувствовал то же самое, что и все мои коллеги-математики. Хотя нам говорят, что «прошлое – это чужая страна» [70], она не может быть чужой во всех отношениях. Люди, о которых мы читаем у Гомера и в Библии, очень похожи на нас. То же самое, по-видимому, верно и в отношении древнегреческих математиков, по крайней мере Архимеда, единственного, кто впустил нас в свое сердце.

Двадцать два века назад, написав письмо своему другу Эратосфену, библиотекарю в Александрии, Архимед, по сути, отправил ему математическое послание в бутылке, которое тогда практически никто не мог оценить, но он надеялся, что оно благополучно преодолеет моря времени. Он делился своей интуицией, своим методом, желая, чтобы он помог будущим поколениям математиков «найти другие теоремы, которые не выпали на нашу долю». Шансы были против него. Времена всегда были жестокими. Царства рушились, библиотеки сжигались, рукописи портились. Ни одна копия «Метода» не пережила периода Средневековья. Хотя Леонардо да Винчи, Галилей, Ньютон и другие гении Возрождения и научной революции изучали то, что осталось от трудов Архимеда, у них не было возможности прочитать «Метод». Считалось, что он безвозвратно утерян.

А затем каким-то чудом его нашли.

В октябре 1998 года потрепанный средневековый молитвенник был выставлен на аукцион Christie’s и продан анонимному частному коллекционеру за 2,2 миллиона долларов. Под латинскими молитвами просматривались едва различимые геометрические чертежи и математический текст, написанный на греческом языке в X веке. Книга оказалась палимпсестом: в XIII веке ее пергаментные листы были вымыты и очищены от греческого текста ради написанных поверх литургий на латыни. К счастью, греческий текст не был полностью уничтожен. Это оказалась единственная сохранившаяся копия «Метода» Архимеда [71].

На палимпсест Архимеда [72], как сейчас называют эту рукопись, впервые обратили внимание в 1899 году, когда он находился в православной библиотеке в Константинополе. Ренессанс и научную революцию он пролежал незамеченным в лавре Саввы Освященного недалеко от Вифлеема. Сейчас он находится в художественном музее Уолтерса в Балтиморе, где был с любовью отреставрирован и исследован с применением новейших технологий воссоздания изображений [73].

Наследие Архимеда живо и сегодня [74]. Взгляните на анимированные фильмы [75], которые так любят смотреть наши дети. Персонажи «Шрека», «В поисках Немо» или «Истории игрушек» кажутся такими живыми и настоящими отчасти потому, что воплощают идею Архимеда: любую гладкую поверхность можно надежно аппроксимировать треугольниками. Например, вот три триангуляции головы манекена [76]:

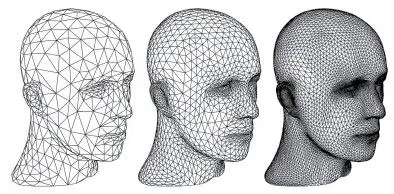
Питер Шрёдер

Чем больше треугольников мы возьмем и чем меньше их размер, тем лучше становится приближение.

То, что верно для манекенов, верно и для огров, и для рыб-клоунов, и для игрушечных ковбоев. Подобно тому как Архимед использовал мозаику из бесконечного количества осколков, чтобы представить сегмент гладкой криволинейной параболы, современные аниматоры из DreamWorks создают круглый живот Шрека и его милые трубообразные уши из десятков тысяч многоугольников. Еще больше потребовалось для сцены турнира, где Шрек [77]сражался с местными громилами: каждый ее кадр требовал свыше 45 миллионов многоугольников [78]. Но в готовом фильме их следов нигде нет. Как учит нас принцип бесконечности, прямое и угловатое может олицетворять изогнутое и гладкое.

Когда примерно через десять лет вышел фильм «Аватар» [79], уровень многоугольной детализации стал запредельным. По настоянию режиссера Джеймса Кэмерона аниматоры использовали около миллиона многоугольников, чтобы изобразить каждое растение в воображаемом мире Пандоры. А учитывая, что действие происходило в пышных виртуальных джунглях, там насчитывалось множество растений… и множество многоугольников. Неудивительно, что производство «Аватара» обошлось в триста миллионов долларов. Это был первый фильм, в котором многоугольники использовались миллиардами [80].

В самых ранних компьютерных анимационных фильмах многоугольников было куда меньше. Тем не менее в то время вычисления казались ошеломляющими. Возьмем «Историю игрушек» [81], вышедшую в 1995 году. Одному аниматору тогда требовалась неделя, чтобы синхронизировать восьмисекундный кадр. На создание всего фильма ушло четыре года и 800 тысяч часов компьютерного времени. Как говорил в интервью журналу Wired соучредитель студии Pixar Стив Джобс, «над этим фильмом работает больше людей с ученой степенью, чем над любым другим в истории кино» [82]. Вскоре после «Истории игрушек» вышел первый анимационный ролик с человеком в главной роли – «Игра Джери» [83]. Эта забавная и грустная история одинокого старичка, который играет сам с собой в шахматы в парке, получила в 1998 году «Оскар» за лучший короткометражный анимационный фильм.

Entertainment Pictures / Alamy

Как и другие персонажи, созданные компьютером, Джери был сконструирован из угловатых форм. В начале этого раздела я показал компьютерную графику лица из все большего количества треугольников. Примерно таким же образом аниматоры студии Pixar смоделировали голову Джери из сложного многогранника, состоявшего из примерно 4500 вершин, соединенных ребрами и гранями, как драгоценный камень. Аниматоры сильнее и сильнее делили эти грани, чтобы получить все более детальное изображение. Этот процесс занял намного меньше компьютерной памяти, чем методы, использованные ранее, и позволял делать анимацию гораздо быстрее [84]. На тот момент это был революционный прорыв в компьютерной анимации, но по духу – продолжение идей Архимеда. Напомним: для того чтобы оценить число π, Архимед начал с шестиугольника, затем перешел к двенадцатиугольнику. После следующего деления получился многоугольник с 24 сторонами, затем 48-угольник и наконец 96-угольник; так происходило постепенное приближение к предельной фигуре – окружности. Точно так же, многократно разделяя свой многогранник, аниматоры Джери аппроксимировали морщинистый лоб персонажа, его торчащий нос и складки кожи на шее. Повторяя этот процесс достаточное количество раз, они смогли сделать Джери таким, каким он должен быть – похожим на куклу персонажем, передающим широкий спектр человеческих чувств.