Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Суть в том, что степенные ряды вооружили Ньютона универсальным инструментом анализа. С ними он мог брать интегралы, находить корни алгебраических уравнений и вычислять значения неалгебраических функций, таких как синусы, косинусы и логарифмы. Как заметил ученый, «с их помощью анализ справляется, я бы сказал, со всеми задачами» [214].

Ньютон как мастер мэшапа

Я не верю, что Ньютон делал это сознательно, но в своей работе со степенными рядами он вел себя как мастер математического мэшапа [215]. Он подошел к задаче площади в геометрии через принцип бесконечности древних греков и сплавил его с индийскими десятичными дробями, исламской алгеброй и французской аналитической геометрией.

Некоторые математические заимствования видны в структуре его уравнений. Например, сравните бесконечный ряд чисел, использованный Архимедом при квадрировании параболы:

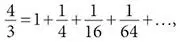
с бесконечным рядом символов, которые Ньютон использует при квадрировании гиперболы:

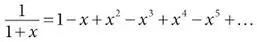
Если вы подставите 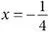в ряд Ньютона, он станет рядом Архимеда. В этом смысле ряд Ньютона вобрал в себя ряд Архимеда как частный случай.

Более того, сходство в их работе распространяется и на рассматриваемые ими геометрические задачи. Оба берут сегменты; Архимед использует свой ряд для квадрирования (нахождения площади) сегмента параболы, а Ньютон – свой усовершенствованный степенной ряд

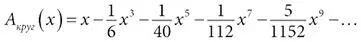
для квадрирования кругового сегмента и другой степенной ряд

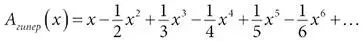
для квадрирования сегмента гиперболы.

На самом деле ряды Ньютона неизмеримо мощнее, чем ряд Архимеда, потому что позволяли находить площади не одного, а бесконечного количества круговых и гиперболических сегментов. Вот что дал ученому абстрактный символ x . Он позволил ему непрерывно и безболезненно менять задачи; менять форму сегментов, сдвигая x влево или вправо, и в результате то, что казалось одним бесконечным рядом, на деле оказывалось бесконечным семейством бесконечных рядов, по одному ряду для каждого конкретного x . Такова мощь степенных рядов. Они дали возможность одним махом решить бесконечно много задач.

Однако повторюсь: Ньютон не решил бы ни одной задачи, если бы не стоял на плечах гигантов. Он объединил, синтезировал и обобщил идеи своих великих предшественников. Он унаследовал принцип бесконечности от Архимеда; научился касательным у Ферма; родиной десятичных дробей была Индия; переменные восходят к арабской алгебре; представление кривых на координатной плоскости позаимствовано из трудов Декарта; раскованные ухищрения с бесконечностью, дух экспериментирования и открытость к допущениям и индукции пришли от Валлиса. Он смешал все это вместе, чтобы создать нечто новое – то, что мы до сих пор используем для решения задач анализа: универсальный метод степенных рядов.

Пока Ньютон работал со степенными рядами зимой 1664–1665 годов, Европу захлестнула страшная эпидемия, двигавшаяся, подобно волне, от Средиземного моря в Голландию. Когда бубонная чума достигла Лондона, она еженедельно убивала сначала сотни, а затем и тысячи людей. Летом 1665 года Кембриджский университет был временно закрыт. Ньютон отправился домой в семейную усадьбу в Линкольншире.

В течение следующих двух лет он стал лучшим математиком в мире. Но изобретения современного анализа было недостаточно, чтобы занять его ум. Он также открыл закон всемирного тяготения (закон обратных квадратов для гравитации) и применил его к движению Луны, изобрел телескоп-рефлектор и экспериментально показал, что белый свет состоит из всех цветов радуги. Ему не было еще и двадцати пяти. Как он позднее вспоминал, «в те дни я был в расцвете сил юности и думал о математике и философии больше, чем когда-либо впоследствии» [216].

В 1667 году, когда чума утихла, Ньютон вернулся в Кембридж и продолжил свои уединенные занятия. К 1671 году он свел разрозненные части анализа в единое целое. Он разработал метод разложения функций в степенные ряды, значительно улучшил существующие теории касательных, используя идеи движения, установил и доказал основную теорему анализа, которая решила задачу площадей, составил таблицы кривых и их функций площадей и свел все это в хорошо настроенную систематизированную вычислительную машину.

Но за стенами Тринити-колледжа он был невидим. Как, собственно, и хотел. Свой секретный источник он держал при себе. Замкнутый и подозрительный, он болезненно относился к критике и ненавидел спорить с кем бы то ни было, особенно с теми, кто его не понимал. Как он позднее объяснял, ему не нравится, когда его «изводят мелкие недоучки в математике» [217].

У него была еще одна причина для беспокойства: он знал, что его работа может быть подвергнута нападкам с точки зрения логики. Он использовал алгебру, а не геометрию и беспечно играл с бесконечностью, первородным грехом анализа. Джона Валлиса, чья книга так повлияла на молодого Ньютона, когда тот был студентом, жестко критиковали за то же самое. Томас Гоббс [218], политический философ и второсортный математик, назвал «Арифметику бесконечного» «паршой символов» [219]за то, что она опирается на алгебру, и «гнусной книгой» [220]за использование бесконечности. И Ньютон должен был признать, что его собственная работа была всего лишь анализом, а не синтезом. Она годилась для открытий, но не для доказательств. Он преуменьшал значение своих методов работы с бесконечностью, считая их «недостойными публичных выступлений» [221], а много лет спустя сказал: «Наша обманчивая алгебра вполне пригодна для поиска результатов, но совершенно не годится для создания текстов и передачи их потомкам» [222].

По этим и другим причинам Ньютон скрывал свои достижения. И все же какая-то его часть жаждала признания. Он был сильно расстроен и подавлен, когда Николас Меркатор опубликовал в небольшой книжке Logarithmotechnia, вышедшей в 1668 году, тот же самый ряд для натурального логарифма, который Ньютон открыл тремя годами ранее. Шок и разочарование оттого, что его опередили, побудили Ньютона написать в 1669 году короткую рукопись и распространить ее частным образом среди его немногих доверенных приверженцев. Книга с полным названием «Анализ с помощью уравнений с бесконечным числом членов» ( De Analysi ) выходила далеко за пределы логарифмов. В 1671 году он расширил ее до своего главного труда по анализу – «Трактата о методах рядов и флюксий», известного также как De Methodis , однако рукопись не увидела свет при его жизни; он тщательно берег ее и хранил для личного пользования. De Analysi была опубликована только в 1711 году, а De Methodis появилась только после смерти ученого, в 1736 году.