Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

В нашей задаче, где x = 2, это уравнение принимает вид

(2 + Δ x ) 3 = 2 3 + 3(2) 2Δ x + 3(2)(Δ x ) 2 + (Δ x ) 3 = 8 + 12Δ x + 6(Δ x ) 2 + (Δ x ) 3.

Теперь мы видим, почему добавка к 8 состоит из трех частей различной величины. Малая, но главная часть равна 12Δ x = 12×0,001 = 0,012. Оставшиеся части 6(Δ x ) 2и (Δ x ) 3отвечают за сверхмалую 0,000006 и сверхсверхмалую 0,000000001 величины. Чем больше множителей Δ x входит в слагаемое, тем оно меньше. Вот почему они ранжируются по размеру. Каждое лишнее умножение на маленькое число Δ x делает малую величину еще меньше.

В этом небольшом примере хорошо видна ключевая идея дифференциального исчисления. Во многих ситуациях, касающихся причины и следствия, дозы и реакции, входа и выхода, а также иной взаимосвязи между переменной x и зависящей от нее переменной y , небольшое изменение на входе Δ x приводит к небольшому изменению на выходе Δ y . Это небольшое изменение, как правило, организовано структурированным способом, который мы можем изучить, а именно: изменение на выходе организовано иерархически из нескольких частей. Они ранжированы по размеру от малого вклада до сверхмалого и еще меньших вкладов. Такая градация позволяет нам сосредоточиться на части, пусть и малой, но вносящей основной вклад, и пренебречь всеми остальными частями – сверхмалыми и еще меньшими. Именно в этом и состоит основная идея. Хотя малое изменение мало, оно колоссально по сравнению с другими (как в нашем примере число 0,12 огромно по сравнению с 0,000006 и 0,000000001).

Такой способ мышления, когда мы пренебрегаем всеми вкладами в правильный ответ, кроме самой крупной, львиной доли, может показаться только приблизительным. И это так, если изменения на входе вроде числа 0,001, добавленного нами к 2, – это конечные изменения. Но если мы рассмотрим бесконечно малые изменения на входе, то наш метод мышления станет точным. Ошибок не будет. Львиная доля становится всем. И, как мы уже говорили в этой книге, бесконечно малые изменения – именно то, что нам нужно, чтобы понимать наклоны, мгновенные скорости и площади криволинейных областей.

Чтобы посмотреть, как это работает на практике, давайте вернемся к примеру выше, когда мы пытались вычислить куб числа, слегка превышающего 2. Только теперь изменим число с 2 на 2+ dx , где dx – бесконечно малое приращение Δ x . Это понятие по своей сути не отличается осмысленностью, так что не думайте о нем слишком усердно. Главное тут – знать, что понимание того, как это работает, упрощает вычисления.

Предыдущая формула (2 + Δ x ) 3 = 8 + 12Δ x + 6(Δ x ) 2 + (Δ x ) 3, в частности, теперь сокращается до более простой:

(2 + dx ) 3 = 8 + 12 dx .

Что произошло с остальными слагаемыми вида 6( dx ) 2 + ( dx ) 3? Мы их отбросили. Ими можно пренебречь. Эти сверхмалые и сверхсверхмалые величины пренебрежимо малы по сравнению с 12 dx . Но почему тогда мы сохранили 12 dx ? Разве эта величина не пренебрежимо мала по сравнению с 8? Да, но если бы мы отбросили еще и ее, то не учли бы вообще никаких изменений, и ответ остался бы 8. Поэтому рецепт таков: для изучения бесконечно малых изменений сохраните слагаемые, включающие dx в первой степени, и игнорируйте все остальные.

Такой способ мышления, использующий бесконечно малые величины вроде dx , можно переформулировать в терминах пределов и сделать совершенно кошерным и строгим. Современные учебники действуют именно так. Но быстрее и проще использовать бесконечно малые величины. Специальный термин для них в этом контексте – дифференциалы Это название проистекает от их представления в виде разностей Δ x и Δ y , когда эти разности в пределе стремятся к нулю [240]. Это похоже на то, что мы видели, когда рассматривали параболу под микроскопом и наблюдали, как кривая становится все прямее и прямее при увеличении.

Позвольте вам показать, насколько простыми становятся некоторые идеи, если подходить к ним через дифференциалы. Например, что такое наклон кривой, если рассматривать ее в виде графика на координатной плоскости? Как мы узнали из нашей работы с параболой в главе 6, наклон – это производная, определяемая как предел Δ y / Δ x , когда Δ x стремится к нулю. А чем он будет в терминах дифференциалов? Просто dy / dx . Словно кривая составлена из крохотных прямых линий.

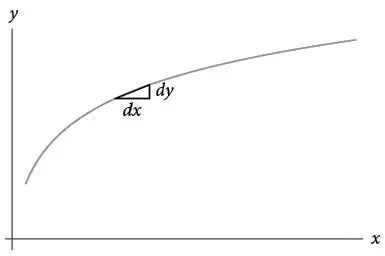
Если мы представим dy как бесконечно малое приращение по вертикали, а dx – как бесконечно малое приращение по горизонтали, то наклон будет просто их отношением, как и всегда для наклонного пандуса, и, следовательно, составит dy / dx .

Чтобы применить этот подход к конкретной кривой (например, y = x 3, которую мы использовали, возводя в куб числа, слегка превосходящие 2), вычислим dy следующим образом. Пишем:

y + dy = ( x + dx ) 3.

Как и раньше, раскрываем скобки справа и получаем

( x + dx ) 3 = x 3 + 3 x 2 dx + 3 x ( dx ) 2 + ( dx ) 3.

Теперь в соответствии с нашим рецептом отбрасываем слагаемые ( dx ) 2и ( dx ) 3, потому что они не входят в львиную долю. Таким образом, у нас получается

y + dy = ( x + dx ) 3 = x 3 + 3 x 2 dx .

А поскольку y = x 3, упрощаем уравнение до вида

dy = 3 x 2 dx .

Деление обеих частей на dx дает соответствующий наклон

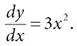
В точке x = 2 это дает наклон 3×(2) 2 = 12. То же число 12, что мы видели ранее. Именно поэтому изменение с 2 до 2,001 давало нам (2,001) 3 ≈ 8,012. Это означает, что бесконечно малое изменение x около 2 (назовем его dx ) преобразуется в бесконечно малое изменение y около 8 (назовем его dy ), которое в 12 раз больше ( dy = 12 dx ).

Между прочим, аналогичные рассуждения показывают, что для любого положительного n производная y = x n равна dy / dx = Δ x n -1; этот результат мы уже упоминали ранее. При небольших дополнительных усилиях мы могли бы распространить его на отрицательные, дробные и иррациональные n .

Большое преимущество бесконечно малых в целом и дифференциалов в частности состоит в том, что они облегчают вычисления. Они срезают путь. Освобождают разум для более творческого мышления, так же как алгебра делала это для геометрии в давние годы. Вот за это Лейбниц и обожал дифференциалы. Он писал своему наставнику Гюйгенсу: «Мой анализ обеспечил мне практически без размышлений огромную часть открытий, которые относятся к этой теме. Что мне больше всего нравится в моем анализе, так это то, что он предоставляет те же преимущества перед древними в геометрии Архимеда, которые Виет и Декарт дали нам в геометрии Евклида или Аполлония, освобождая нас от необходимости работать с воображением» [241].