Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

Единственное, что нехорошо с бесконечно малыми величинами, – это то, что они не существуют, по крайней мере в системе действительных чисел. Да, и еще одно – они парадоксальны. Они не казались бы осмысленными, даже если бы существовали. Один из последователей Лейбница, Иоганн Бернулли, понял, что они обязаны удовлетворять бессмысленным уравнениям вроде x + dx = x , хотя dx – это не ноль. Хм. Ну нельзя же получить все сразу! Бесконечно малые величины действительно дают правильные ответы, как только мы научимся с ними работать, а предоставляемые ими выгоды с лихвой компенсируют все психические расстройства, которые они могут вызывать. Они подобны лжи Пикассо, которая помогает нам осознать истину.

В качестве еще одной демонстрации мощи бесконечно малых величин Лейбниц использовал их для вывода закона синусов для преломления света, предложенного Снеллом. Вспомните главу 4: когда свет переходит из одной среды в другую (скажем, из воздуха в воду), он изгибается в соответствии с математическим законом, который не раз был установлен в течение столетий. Ферма объяснил его своим принципом наименьшего времени, но изо всех сил пытался решить задачу оптимизации, которую подразумевал его принцип. С помощью своих дифференциалов Лейбниц с легкостью вывел закон синусов [242]и с явной гордостью отметил, что «другие весьма ученые мужи искали многими хитроумными способами то, что человек, сведущий в этом анализе, может достичь в этих строках, как по волшебству» [243].

Основная теорема анализа через дифференциалы

Еще одним триумфом дифференциалов Лейбница стало то, что они сделали основную теорему прозрачной. Вспомним, что она относится к функции накопления площади A ( x ), которая определяет площадь под кривой y = f ( x ) в интервале от 0 до x . Теорема гласит, что при сдвиге x вправо площадь под кривой накапливается со скоростью самой f ( x ). Таким образом, f ( x ) является производной A ( x ).

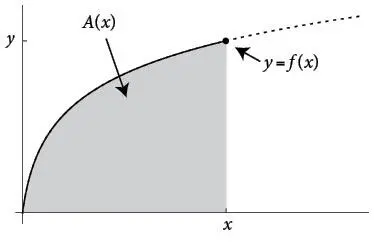
Чтобы понять, откуда берется этот результат, предположим, что мы увеличиваем x на бесконечно малую величину dx . Как изменится площадь A ( x )? По определению, она изменится на величину dA , то есть новая площадь равна старой плюс ее приращение, A + dA .

Основная теорема получается сразу же, как только мы наглядно представим, чему должно равняться dA . Как видно из рисунка ниже, площадь изменяется на бесконечно малую величину dA , которая представляет собой узкую вертикальную полоску между x и x + dx .

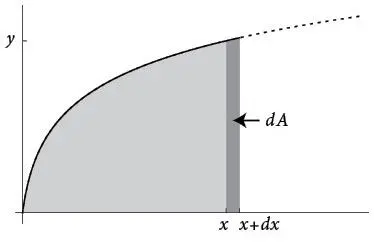
Эта полоска – прямоугольник с высотой y и основанием dx . Поэтому его площадь равна произведению этих величин, то есть y dx или, если угодно, f ( x ) dx .

В действительности такая полоска будет прямоугольником только при бесконечно малом приращении. В реальности для полоски конечной ширины Δ x изменение площади Δ A будет состоять из двух частей. Основной вклад внесет прямоугольник площади y Δ x . Намного меньше по площади маленький, криволинейный сверху, похожий на треугольник кусочек, располагающийся над этим прямоугольником.

Вот еще один случай, когда мир бесконечно малых величин приятнее реального. В реальном мире нам пришлось бы учитывать площадь этой крышечки, а это сделать непросто, поскольку она зависит от формы кривой. Но когда ширина прямоугольника стремится к нулю и «становится» dx , площадь крышечки оказывается пренебрежимо малой по сравнению с площадью прямоугольника. Это сверхмалая величина по сравнению с малой величиной.

В результате получается, что dA = y dx = f ( x ) dx . Бум! И вот вам основная теорема анализа. Или, как это более вежливо переформулируют в нынешние дни (в наше заблудшее время, когда дифференциалы отвергнуты ради производных),

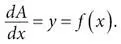
Это в точности то, что мы установили в главе 7 с помощью примера с малярным валиком.

И последнее: когда мы рассматриваем площадь под кривой как сумму бесконечного числа бесконечно узких прямоугольных полосок, то записываем это как [244]

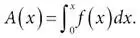
Этот символ с длинной шеей, похожий на лебедя – фактически растянутая буква S , которая напоминает нам, что здесь происходит суммирование [245]. Это суммирование определенного рода, характерное для интегрального исчисления, подразумевающее сумму бесконечного количества бесконечно узких полосок, объединенных в единую связную область. Символ называется знаком интеграла. Лейбниц ввел его в рукописи 1677 года и опубликовал в 1686-м. Это самый узнаваемый символ математического анализа. Число 0 под этим знаком и величина x над ним указывают на конечные точки интервала на оси x , над которым выстроены прямоугольники. Эти точки называются пределами интегрирования.

Как Лейбниц пришел к дифференциалам и основной теореме?

Ньютон и Лейбниц пришли к основной теореме анализа разными путями. Ньютон – размышляя о движении, постоянном спутнике математики. Лейбниц же зашел с другой стороны. Хотя у него не было математического образования, ранее он какое-то время занимался целыми числами, сочетаниями и перестановками, а также дробями и суммами определенного рода.

Более глубоко погружаться в эту науку он начал после встречи с Христианом Гюйгенсом. В то время Лейбниц находился с дипломатической миссией в Париже и был очарован рассказами Гюйгенса о последних достижениях в математике, поэтому захотел узнать больше. С чудесной педагогической прозорливостью (или это была удача?) Гюйгенс поставил перед учеником задачу, которая и привела немецкого математика к основной теореме [246].

Гюйгенс предложил Лейбницу вычислить бесконечную сумму:

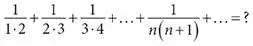
(Точки в знаменателе означают умножение.) Чтобы понять задачу, начнем для разминки с простого варианта. Предположим, что сумма не бесконечна, а содержит, скажем, только 99 слагаемых. Иными словами, нам нужно вычислить

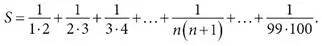
Если вы не найдете какого-то хитроумного трюка, то расчеты будут утомительными, хотя и несложными. При достаточном терпении (или при наличии компьютера) и упорстве можно сложить все 99 дробей. Однако пропала бы суть, а она тут в том, чтобы найти элегантное решение. Элегантные решения ценятся в математике не только потому, что красивы, но и потому, что сильны. Проливаемый ими свет часто можно использовать для решения других задач. В нашем случае элегантный свет, быстро обнаруженный Лейбницем, позволил ему открыть основную теорему анализа.