Стивен Строгац - Бесконечная сила [Как математический анализ раскрывает тайны вселенной]

В конце первой стадии вирусная нагрузка стабилизируется на определенном уровне, который, как ни странно, может поддерживаться годами. Врачи называют этот уровень точкой отсчета. Пациент без лечения может прожить десяток лет без ВИЧ-симптомов, а данные лабораторных исследований ничего не покажут, кроме постоянной вирусной нагрузки и низкого, постепенно падающего количества T-лимфоцитов. Однако в итоге бессимптомная стадия заканчивается и начинается СПИД, для которого характерно дальнейшее снижение количества T-лимфоцитов и резкое повышение вирусной нагрузки. Как только у нелеченого больного развивается полномасштабный СПИД, оппортунистические инфекции, рак и иные осложнения обычно приводят к его смерти за два-три года.

Ключ к разгадке тайны находился в длительной бессимптомной стадии. Что происходит в это время? Спит ли ВИЧ в организме? Другие вирусы, как известно, впадают в спячку. Например, вирус генитального герпеса скрывается в нервных узлах, чтобы ускользнуть от иммунной системы. Вирус ветряной оспы делает то же самое, годами скрываясь в нервных клетках, но иногда просыпаясь и вызывая опоясывающий лишай. Причина латентности ВИЧ была неизвестна, однако Хо и Перельсон ее выяснили.

В ходе исследования 1995 года они давали больным ингибитор протеазы не в качестве лечения, а для сбора сведений. Прием препарата провоцировал активную реакцию организма пациента, что и позволило Хо и Перельсону – впервые в истории – отследить динамику иммунной системы в борьбе с ВИЧ. Они обнаружили, что после приема ингибитора протеазы количество вирусных частиц в организме больного падало экспоненциально быстро. Скорость снижения была невероятной: иммунная система каждые два дня выводила половину всех вирусных частиц в кровотоке.

Дифференциальное исчисление позволило Хо и Перельсону смоделировать это экспоненциальное снижение и извлечь из него удивительные следствия. Сначала они представили изменяющуюся концентрацию вируса в крови как неизвестную функцию V ( t ), где t – время после введения ингибитора протеазы. Затем они выдвинули гипотезу об изменении концентрации вируса dV за бесконечно малый интервал времени dt . Их данные указывали на то, что каждый день из крови удаляется постоянная доля вируса, так что, возможно, это свойство сохранится и при экстраполяции на бесконечно малые интервалы dt . Поскольку величина dV / V – это относительное изменение концентрации вируса, их модель можно было записать символами в виде такого уравнения:

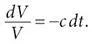
Здесь коэффициент пропорциональности c – это скорость выведения, мера того, насколько быстро организм избавляется от вируса.

Приведенное уравнение – пример дифференциального уравнения. Оно связывает дифференциал функции dV с самой функцией V , а также с дифференциалом dt времени. Проинтегрировав обе части с помощью основной теоремы, Перельсон и Хо решили его относительно V ( t ) и обнаружили, что справедливо соотношение

ln[ V ( t ) / V 0] = – ct ,

где V 0 – первоначальная вирусная нагрузка, а ln – натуральный логарифм (та самая логарифмическая функция, которую изучали Ньютон и Меркатор в 1660-е годы). Отсюда можно найти, что

V ( t ) = V 0 e - ct ,

где e – основание натуральных логарифмов. Это подтверждало, что вирусная нагрузка в модели действительно снижалась экспоненциально. Наконец, подобрав экспоненту в соответствии с экспериментальными данными, Хо и Перельсон оценили ранее неизвестное значение скорости выведения c .

Для тех, кто предпочитает использовать производные, уравнение модели можно записать так:

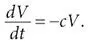
Здесь dV / dt – это производная V . Она показывает, насколько быстро растет или падает концентрация вируса. Положительное значение производной означает повышение, отрицательное – снижение. Поскольку концентрация V положительна, величина – cV должна быть отрицательной, поэтому и производная должна быть отрицательной, что означает снижение концентрации, как и показал эксперимент. Кроме того, пропорциональность между dV / dt и V означает, что чем ближе V к нулю, тем медленнее спад. На интуитивном уровне это замедление спада V подобно тому, что происходит, когда вы наполняете раковину водой, а затем открываете сток. Чем меньше воды в раковине, тем медленнее она стекает, поскольку уменьшается давление воды, заставляющее ее течь. При такой аналогии количество вируса подобно количеству воды, а стекание – оттоку вируса в результате работы иммунной системы.

Смоделировав действие ингибитора протеазы, Перельсон и Хо скорректировали свое уравнение, чтобы описать условия до введения препарата. Они предположили, что уравнение будет иметь вид

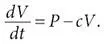
В этом уравнении P означает исходный (не замедленный) темп репродукции вирусных частиц – еще один параметр, неизвестный в то время. Перельсон и Хо предполагали, что до введения ингибитора протеазы в каждый момент зараженные клетки продуцировали новые вирусные частицы, которые потом заражали новые клетки, и так далее. Именно возможность такого взрывного распространения и делает ВИЧ настолько разрушительным.

Однако на бессимптомной стадии, похоже, существует некое равновесие между воспроизводством вируса и его выведением иммунной системой. На этом установившемся уровне вирус размножается с такой же скоростью, как и выводится. Это позволило понять, почему вирусная нагрузка может не меняться годами. В аналогии с водой это подобно происходящему при одновременном открытии и крана, и стока. Вода достигает стабильного уровня, когда поступление жидкости равно ее оттоку.

Если на некотором уровне концентрация вируса не меняется, то ее производная должна быть равна нулю: dV / dt = 0. Следовательно, стабильная вирусная нагрузка удовлетворяет соотношению

P = cV 0.

Перельсон и Хо использовали это простое уравнение, чтобы оценить жизненно важный параметр, который никто не мог измерить ранее: количество вирусных частиц, ежедневно удаляемых иммунной системой. Оказалось, что эта величина – миллиард вирусных частиц в день.

Число получилось неожиданно огромным и впечатляющим. Оно указывало на то, что во внешне, казалось бы, спокойные десять лет бессимптомной стадии в организме больного ежедневно происходит титаническая борьба. Каждый день иммунная система выводит миллиард вирусных частиц, а зараженные клетки порождают миллиард новых. Иммунная система вела яростную тотальную войну с вирусом и боролась с ним практически до полной остановки.