Ирина Краева - Математический календарь. Инструкция по созданию

Дата (число и номер месяца), когда отмечают день квадратного корня, соответствует однозначному числу, квадратом которого и оканчивается номер года.

Перечислим официальные 3 3 Официальные, потому что далее мы рассмотрим возможности отмечать дни квадратного корня каждый год. Но уже, так сказать, «не официально». дни квадратного корня, уже состоявшиеся в этом веке: 1 января 2001, 2 февраля 2004, 3 марта 2009, 4 апреля 2016.

Ожидают нас такие праздники квадратного корня:

5 мая 2025 года

6 июня 2036 года

7 июля 2049 года

8 августа 2064 года

9 сентября 2081 года.

Так как по понятным причинам время наступления этих дат сильно ограничено, следует помнить о них, чтобы не пропустить такое редкое событие в календаре математики.

На наш взгляд, нет причины не отметить день квадратного корня 10 октября 2100 года, 11 ноября 2121 года и 12 декабря 2144. Но эти даты пока за гранью нашего текущего восприятия действительности.

Это даже не праздник, как таковой, а именно мгновение. Конкретная секунда конкретного дня.

Если записать в формате <���час>, <���минуты>, <���секунды>, <���день>, <���месяц>, <���год>, то должны получиться шесть натуральных последовательных чисел. Например, 8.9.10/11.12.13 – восемь часов девять минут и десять секунд одиннадцатого декабря 2013 года (ну или 1913, а может 2113, возможны варианты). Или, 16.15.14/13.12.11.

Можно пойти на обобщение и говорить не о «последовательных натуральных числах», а о «последовательных чётных числах» или «последовательных нечётных числах». А ещё надо учесть в каком порядке числа можно записать – возрастающем или убывающем.

Но всё равно, по этим правилам не так много интересных мгновений получится. И понятно, что такие возможности в этом веке уже закончились (так как номера месяцев ограничены числом 12).

К придуманным праздникам, наступающим в один и тот же день каждого года, отнесём, прежде всего, дни однозначных натуральных чисел.

Эти даты таковы, что номер дня и номер месяца совпадают:

1 января – День Единицы

2 февраля – День Двойки

3 марта – День Тройки

4 апреля – День Четвёрки

5 мая – День Пятёрки

6 июня – День Шестёрки

7 июля – День Семёрки

8 августа – День Восьмёрки

9 сентября – День Девятки.

К этим датам мы ещё вернёмся, потому что они, как оказалось, обладают весьма существенным потенциалом.

Далее, как было сказано в предисловии, мы установили ещё три праздника:

10 октября – День Десятичной Системы Счисления

11 ноября – День Замечательных Чисел и Констант

12 декабря – День Дюжины.

По аналогии с числом π назначим праздник для другого замечательного числа:

7 февраля(2.7) – День числа е .

Существуют в каждом году даты, которые есть смысл назвать днями Шехерезады: 10 января(10.01), 20 февраля(20.02) и 30 марта(30.03): число 1001 носит имя «число Шехерезады» (помните? «Тысяча и одна ночь»…). Число Шехерезады занимательно тем, что кратно 7, 11 и 13.

Так как дней Шехерезады три штуки, то мы как-то в один год решили каждому дать название: 10.01 – чудесный день, 20.02 – волшебный день, 30.03 – магический день.

28 июняпусть будет днём совершенного числа, потому что и 6 и 28 являются первыми совершенными числами.

Дни второйстепени – 1 января, 2 апреля, 3 сентября.

День третьейстепени – 1 января, 2 августа.

Ежегодные Дни квадратных корней 4 4 Как вы помните, мы назвали их «неофициальными». – 1 января, 4 февраля, 9 марта, 16 апреля, 25 мая.

Кроме того, бросим взгляд в прекрасное далёко: почему бы не праздновать дни квадратного корня 19 июня 2114 года (просто 2014 уже прошёл), 22 мая 2115 года, 25 июня 2116 года и 28 сентября 2117 года?

Почему в эти дни? А смотрите на рисунке!

8 августа – День Бесконечности.

31 мая – День однозначного числа(3 +1 +5 = 9) 5 5 Праздник надуманный, но уж очень интересно выходит, что сумма цифр даты равна наибольшему однозначному числу! .

29 сентября – дата года с максимально возможной суммой цифр (20), а 1 января – с минимальной (2). Но у первого января оказалось столько «праздничного» наполнения, что нет смысла нагружать его ещё и этим смыслом.

А теперь снова о датах, в которых номер дня совпадает с номером месяца.

Кроме ежегодных Дней однозначных чисел, они, к примеру, могут быть днями среднего квадратичного или среднего гармонического (об этом подробнее далее).

А также в эти дни можно зарядить забаву: с помощью одной конкретной цифры записать номер года.

Само по себе задание не такое уж сложное: если совсем уж в лоб, то 2023 =

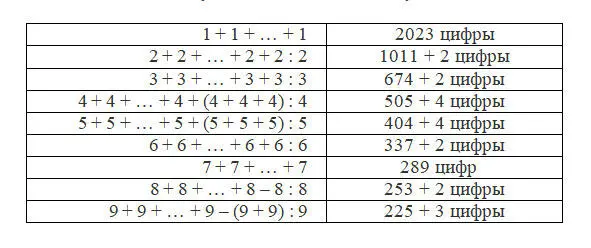
Но! Можно установить правило: чем меньше цифр, тем лучше. И тогда можно начать креативить, например, объединяя цифры в многозначные числа:

2023 = 1111 +111 × (1 +1) × (1 +1) × (1 +1) +11 +11 +1 +1;

2023 = (222 +222) × 2 × 2 +222 +22 +2 +2: 2;

2023 = (333 +333) × 3 +3 × 3 × 3 – (3 +3): 3;

2023 = 444 × 4 +44 × 4 +44 +4 × 4 +4 +4 + (4 +4 +4): 4;

2023 = 555 +555 +555 +55 × 5 +55 +5 × 5 + (5 +5 +5): 5;

2023 = 666 +666 +666 +6 × (6 – 6: 6) – (6 – 6: 6);

2023 = 777 +777 +77 × (7 – 7: 7) +7;

2023 = 888 +888 +88 +88 +8 × 8 +8 – 8: 8;

2023 = 99 × (9 × 9 + (9 +9): 9) +9 +9 +9 +9 +9 – (9 +9): 9.

Но и это не предел. Высший пилотаж, когда результат достигается с помощью только четырёх знаков арифметических действий и скобок.

В некоторых случаях значительно уменьшить количество используемых цифр позволяет знак факториала и двойного факториала. И разрешение на возведение в степень порой существенно продвигает дело.

В октябре 2022 года в сообществе ВК «Математические лайфхаки» 6 6 Ссылка на группу https://vk.com/metodikamatematiki312 в рамках математической предновогодней стодневки был проведён как раз такой конкурс для числа 2023, итоги которого представляем.

Уточним, что использование только скобок и знаков арифметических действий приравнивалось к высшей лиге; скобок, знаков арифметических действий и знака факториала – к первой; скобок, знаков арифметических действий, факториала и возведения в степень – ко второй.