Владимир Трошин - Натуральные числа. Этюды, вариации, упражнения

если сумма собственных делителей больше самого числа ( + sn > n ), то число называется избыточным ;

если свершится чудо и сумма собственных делителей будет равна самому числу ( + sn = n ), то число называется совершенным !

Следует отметить, что древние греки, от которых идут основы теории чисел, не считали само число его делителем. Чтобы наглядно прочувствовать разбиение натуральных чисел на отдельные виды, нужно поработать с числами. Возьмем для примера первые 100 чисел натурального ряда. Вычислим делители каждого из чисел, найдем количество делителей, сумму всех делителей числа и сумму собственных делителей. После этого можно будет сделать некоторые выводы о количестве тех или иных чисел в первой сотне.

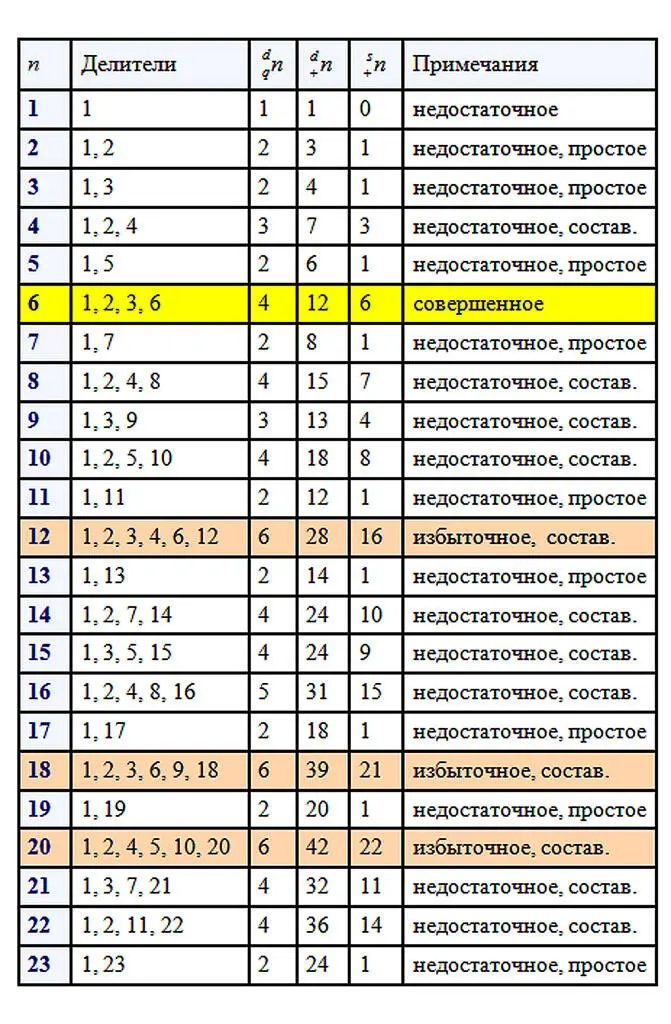
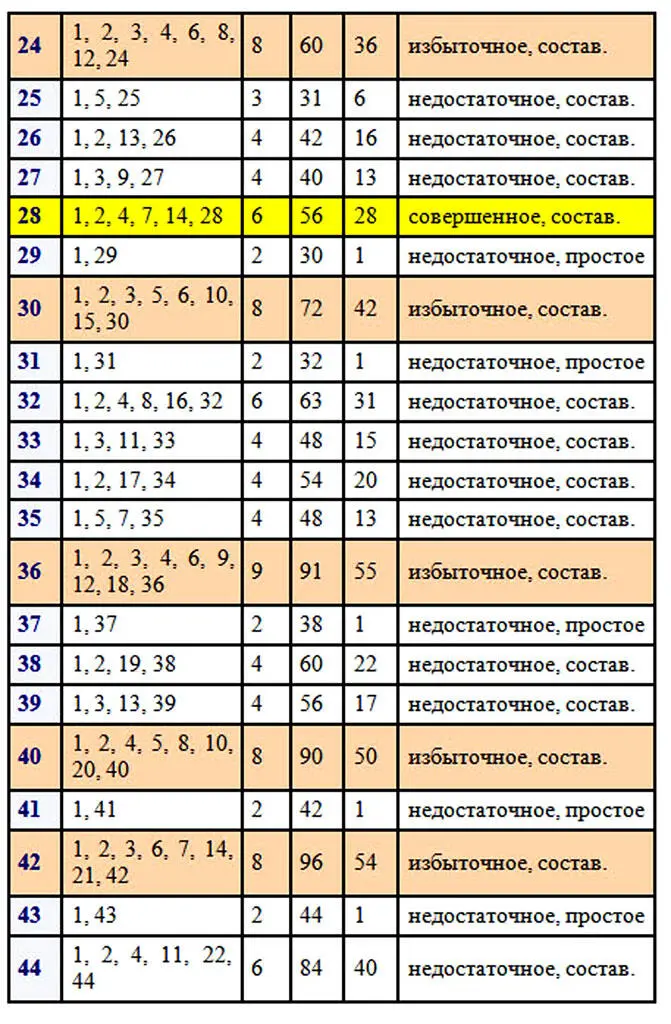
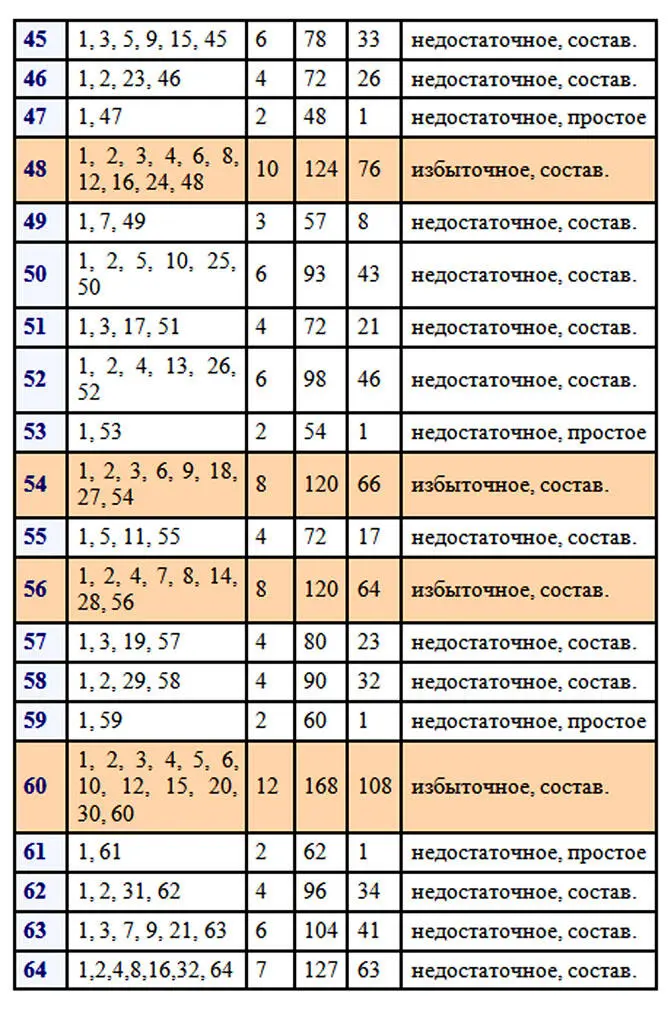
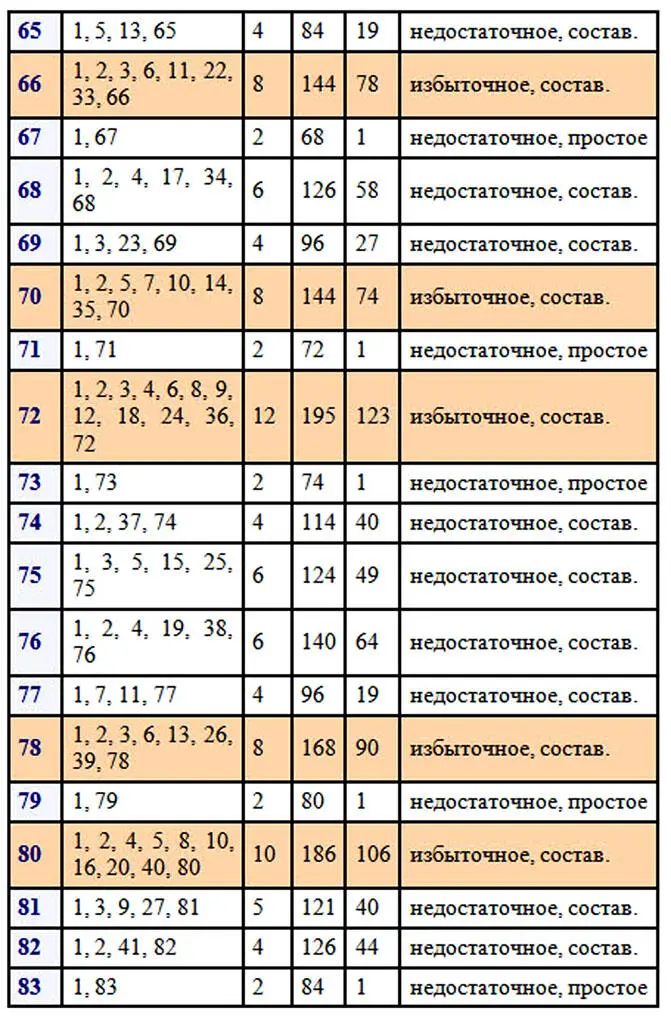
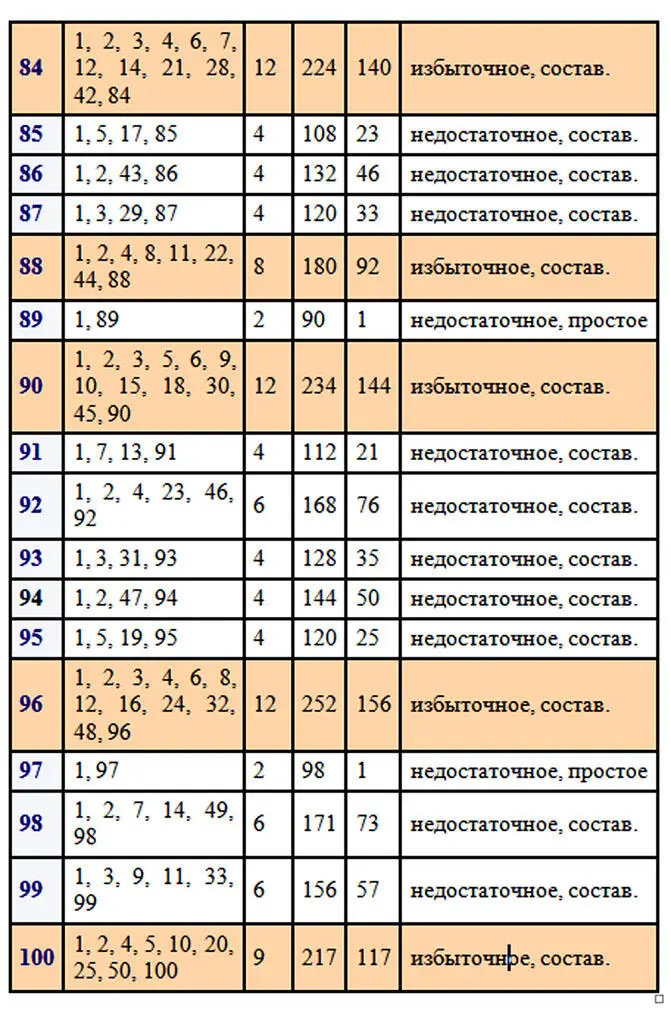
В первой сотне выявлено только два совершенных числа 6 и 28. Совершенные числа – это большая редкость.

Простых чисел в первой сотне 25. Исключаем единицу, как не относящуюся ни к простым числам, ни к составным, следовательно, в первой сотне 74 составных числа. Составных чисел больше и отношение количества составных чисел к количеству простых равно 74/25=2,96.

Избыточных чисел в первой сотне 22, недостаточных больше, их 75. Отношение количества недостаточных чисел к количеству избыточных равно 75/22=3,4(09). Как много бедных, как мало богатых…, среди чисел, разумеется. Эти соотношения меняются в зависимости от рассматриваемого отрезка натурального ряда чисел. В интернете можно найти таблицу делителей натуральных чисел от 1 до 1000 и даже до 10 000. Для множества в тысячу чисел результаты следующие: простых чисел 168, следовательно, составных 831 и соотношение равно 831/168=4,95.

Рассмотрим поближе избыточные числа: 12, 18, 20, 24, 30, 36, 40, 42, 48, 54, 56, 60, 66, 70, 72, 78, 80, 84, 88, 90, 96, 100 … .

Существует бесконечно много как чётных, так и нечётных избыточных чисел. Уверяю вас, это утверждение доказано, но посмотрите на перечисленные избыточные числа первой сотни! Не в пору ли усомниться в сказанном, где среди них нечетные числа? Их нет. Наименьшим избыточным числом является 12, это мы видим в приведенной таблице. Оказывается, избыточные нечетные числа более редкая вещь и чтобы найти наименьшее из них пришлось бы перебирать числа первой тысячи, так как наименьшим нечетным избыточным числом является 945, которое стоит на 386-ом месте среди избыточных чисел. В тексте будут попадаться задания для читателей отмеченные цифрой и знаком вопроса. На такие задания в конце книги даются ответы.

1?. Какое следующее по порядку нечетное избыточное число из бесконечного множества нечетных избыточных чисел?

Попробуйте найти сами. Подскажу только, что и во второй тысяче есть только одно нечетное избыточное число, в третьей тысяче их два и так далее. Довольно редкие создания. Если говорить о множестве всех натуральных чисел, то почти каждое четвёртое натуральное число является избыточным. Более точно установлено, что произвольно взятое натуральное число является избыточным с вероятностью, лежащей между 0,2474 и 0,2480.

Интересную закономерность доказал советский математик Лев Шнирельман: любое натуральное число, большее 28 123, может быть представлено в виде суммы двух избыточных чисел. Видите, работают люди с натуральными числами, находят новые закономерности. Нам и далее будут встречаться закономерности и проблемы, связанные со сложением чисел, их называют аддитивными, в отличие от вопросов, связанных с умножением, называемых мультипликативными. Почему-то аддитивных проблем в теории чисел больше, видимо, это заложено в аддитивном принципе получения множества натуральных чисел. Таким образом, Лев Шнирельман доказал одну из аддитивных теорем.

Нельзя обойти вниманием недостаточные числа. Их гораздо больше, чем избыточных, поэтому им всегда уделяли меньше внимания, никакой благотворительности, сами пусть разбираются, почему они недостаточные. Вот сколько недостаточных набралось среди первых пятидесяти чисел: 1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 46, 47, 49, 50. Существует бесконечно много как чётных, так и нечётных недостаточных чисел. Но обратите внимание, нечетные числа среди недостаточных чисел встречаются гораздо чаще четных в отличие от чисел избыточных. Тоже ведь интересно, почему образовалось такое распределение? Возможно потому, что к недостаточным числам относятся все простые числа (так как у них только один собственный делитель – это единица), а также степени простых чисел и собственные делители недостаточных и совершенных чисел.

Переходим в область редко встречающихся чисел и поговорим о редкостях, превосходящих в своей исключительности даже нечетные избыточные числа. Совершенные числа были известны как древним грекам, так и математикам древнего Востока. До Евклида были известны только два совершенных числа, которые находятся в первой сотне натуральных чисел: 6 и 28. Евклид вывел формулу для получения четных совершенных чисел, он доказал, что четное совершенное число имеет вид 2 p -1·(2 p -1), где p простое число и при этом 2 p -1 также должно быть простым. Используя эту формулу, он нашел третье и четвертое совершенные числа при p =5 и p =7.

2 5-1·(2 5-1)=16·(32-1)=16·31=496;

2 7-1·(2 7-1)=64·(128-1)=64·127=8 128.

Формула Евклида позволяет без труда доказывать многочисленные свойства совершенных чисел. Все совершенные числа треугольные (об этом дальше). Это значит, что, взяв совершенные число шаров, мы всегда сможем сложить из них равносторонний треугольник. Все совершенные числа, кроме 6, можно представить в виде частичных сумм ряда кубов последовательных нечетных чисел: 1 3+3 3+5 3+ … . Впоследствии Леонард Эйлер строго доказал, что все чётные совершенные числа имеют вид, указанный Евклидом. В первой сотне их оказалось всего два, а далее они отстоят друг от друга все дальше и дальше. Почти полторы тысячи лет люди знали только четыре совершенных числа. Трудность состояла не в том, чтобы подставить в формулу очередное простое p , а в том, чтобы проверить простоту 2 p -1. Требовались большие по объему вычисления, а вычислительной техники не существовало. Только в XV веке смогли обнаружить пятое совершенное число 33 550 336, соответствующее p =13 в формуле Евклида. Сделал это немецкий математик Региомонтан. В следующем веке немецкий учёный Шейбель нашел ещё два совершенных числа: 8 589 869 056 и 137 438 691 328. Они соответствуют p =17 и p =19. Независимо от него на совершенство этих чисел указывали итальянец Катальди и француз Марин Мерсенн.