Питер Эткинз - Десять великих идей науки. Как устроен наш мир.

Если под красотой мы имеем в виду симметрию и контролируемые нарушения симметрии, Мондриана, переходящего в Моне, то красота, конечно, лежит в сердце мира. Часть этой красоты открыта для непосредственного восприятия, например, когда мы смотрим на прекрасное произведение искусства. Другая часть, однако, глубоко спрятана и неочевидна для необученного взгляда. Тысячи лет, прошедшие со времени Поликлита, были использованы для того, чтобы выкопать скрытую красоту, дать ее оценку в математической форме, и затем, используя математические средства, провести более глубокие раскопки ландшафта реальности. Как я уже подчеркивал, по мере развития науки, ее глубина и богатство возрастают за счет увеличения абстрактности ее концепций. Это возрастание нигде не прослеживается лучше, чем в открытии симметрии и в развернутом ее использовании в качестве инструмента познания.

Теперь я проведу вас, настолько подробно, насколько мне удастся, по пути, ведущем от непосредственно воспринимаемого к воображаемому, и продемонстрирую ту власть, которую дает в наши руки симметрия. Этот путь поведет нас на самый край обрыва того, что еще доступно воображению.

Объект является симметричным, если действие — которое мы называем преобразованием симметрии , — произведенное над ним, оставляет его неизменным по внешнему виду. Другими словами, если вы на мгновение закроете ваши глаза, то когда вы откроете их снова, вы не сможете сказать, совершил я какое-либо действие или нет. Представьте себе гладкий мяч без украшений; закройте на мгновение глаза, откройте их: повернул ли я шар? Действия, которые мы рассматриваем, могут быть вращением вокруг оси или отражением в зеркале, но существуют и другие преобразования симметрии, которые нам еще предстоит оценить, некоторые из которых представляют собой составные комбинации более простых действий, например, движение в пространстве (называемое трансляцией ), за которым следует отражение в зеркале. Вы можете найти отражение даже в музыке. Одним особенно прозрачным примером является поддельное двухчастное сочинение «Моцарта», которое начинается так

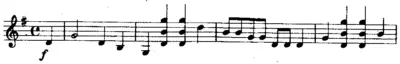
и завершается второй частью

являющейся отражением первой части.

Некоторые объекты являются более симметричными, чем другие. Сфера в высокой степени симметрична — это один из самых симметричных объектов, с которыми мы обычно сталкиваемся. Подумайте о числе способов, которыми я могу изменить положение сферы, пока ваши глаза закрыты, так, что вы не сможете обнаружить это, открыв глаза. Я могу повернуть ее вокруг любой из бесконечного числа осей, проходящих через ее центр, на любой угол, лежащий между 0 и 360°. И это еще не все. Я могу представить себе зеркало, проходящее через центр сферы в любом из бесконечного числа направлений, и вы не сможете обнаружить отражение одной полусферы в другую. Есть и другие действия, которые я могу произвести в уме: я могу вообразить, что я беру каждый атом шара на прямой линии, проходящей через центр сферы, и перемещаю этот атом на равное расстояние от центра сферы с другой стороны. Таким путем я перестраиваю шар с помощью операции, известной как инверсия . Вы не сможете утверждать, что я проделал это, поскольку шар после такой инверсии выглядит точно таким же, каким был вначале.

Куб гораздо менее симметричен, чем сфера. Существует несколько действий, которые я могу над ним произвести так, чтобы вы об этом не узнали. Я могу повернуть куб на 90° и 180° по часовой стрелке и против нее вокруг оси, проходящей через центры любой из трех пар противоположных граней. Я могу повернуть его на 120° по часовой стрелке и против нее вокруг любой из четырех осей, проходящих через противоположные углы. Я могу отразить его от любой из трех плоскостей, в которой я могу поместить зеркало, разрезающее куб пополам. Я могу перестроить куб с помощью инверсии относительно его центра. Я бы мог даже оставить куб нетронутым: вы бы не узнали. Поэтому ничегонеделание — называемое тождественным преобразованием — тоже является преобразованием, которое я должен включить в рассмотрение симметрии объекта. Это дает много различных действий, которые я могу проделать так, чтобы вы не узнали; поэтому куб является высоко симметричным, но совсем не таким симметричным, как сфера, с ее бесконечным числом незразличимых преобразований.

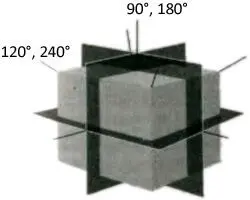
Рис. 6.1.Некоторые из преобразований симметрии для куба. Куб выглядит неизмененным, когда мы вращаем его на 90° или 180° вокруг осей, перпендикулярных каждой грани, и на 120° или 240° вокруг осей, проходящих через противоположные углы. Он также выглядит неизмененным при отражении относительно любой из изображенных здесь плоскостей. Есть еще два преобразования симметрии: инверсия относительно центра куба и тождественное преобразование (ничегонеделание).

С определенной формальной точки зрения симметрично все. Это так, потому что в число рассматриваемых преобразований симметрии мы включили тождественное преобразование; ведь даже самые несимметричные объекты — смятый газетный лист, например, — как мы можем проверить, выглядят также, если мы откроем глаза после того, как с ними ничего не было сделано. В данный момент это может показаться жульничеством, что, конечно, так и есть. Однако включение тождественного преобразования вводит все объекты в сферу действия математической теории симметрии, так что мы можем пользоваться соображениями симметрии при обсуждении чего угодно, а не только объектов, о которых мы думаем, как о «симметричных». Математика вообще действует таким образом: она обобщает определения, чтобы ее теоремы могли охватить настолько большую область, насколько это возможно. Конечно, хотя все и симметрично (в этом формальном смысле), некоторые вещи более симметричны, чем другие. «Более симметричные» просто означает, что существует больше способов их изменения, таких, что, когда мы откроем глаза, мы не сможем сказать, было произведено действие или нет. Сфера более симметрична, чем куб, а куб более симметричен, чем пальма. Как можно видеть, теперь мы способны упорядочить объекты в соответствии со степенью их симметрии: аромат симметрии обретает число.

Математическая теория симметрии, в которой этот аромат отвердевает в точных определениях, называется теорией групп . Название этой теории возникло из того факта, что преобразования симметрии, о которых мы говорили, образуют множества операций, которые в математике называются группами. Вообще говоря, группа состоит из множества элементов и правила их комбинирования, такого, что комбинация любой пары элементов тоже является элементом этого множества. Мы можем увидеть, как преобразования симметрии формируют группу, снова представив себе куб. Предположим, я последовательно провожу два действия, поворачивая куб на 90° вокруг одной из осей, перпендикулярных грани, а затем вращая получившийся куб на 120° вокруг диагональной оси. Результат оказывается таким же, каким бы он был, если бы я повернул куб на 120° вокруг одной из других диагональных осей, поэтому эти два последовательно выполненных преобразования эквивалентны одному преобразованию симметрии. Это верно для всех преобразований симметрии куба, поэтому эти преобразования образуют группу. Группам преобразований симметрии для различных фигур даны названия. Например, огромная группа симметрии сферы называется SO(3). Позже мы встретим другие группы с названиями типа SU(2) и SU(3).