Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании
- Название:Maple 9.5/10 в математике, физике и образовании
- Автор:
- Жанр:
- Издательство:СОЛОН-Пресс
- Год:2006
- Город:Москва
- ISBN:5-98003-258-4
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании краткое содержание
Книга является справочником и руководством пользователя по новейшим системам символьной (аналитической) математики — Maple 9.5 и Maple 10. Это признанные мировые лидеры в области аналитических вычислений, прошедшие серьезную сертификацию в этой области. Кратко описан интерфейс систем и подробно их обширные возможности в математике, физике и образовании. Особое внимание уделено технике практических вычислений и визуализации их результатов, а также решению дифференциальных уравнений различного типа. Описаны средства символьных и численных вычислений, графические и программные возможности систем, пакеты их расширения, маплеты и практика применения Maple в математических и физических расчетах. Прилагаемый CD-ROM содержит более 340 файлов с примерами вычислений. Для научно-технических работников, студентов и преподавателей университетов и вузов.
Maple 9.5/10 в математике, физике и образовании - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
Пожалуй, самым распространенным оператором является оператор присваивания :=. Он используется для задания переменным конкретных значений, например:
> х:=у;
> у:=z;
> z:=2;
> х;
> у;
Этот простой пример наглядно иллюстрирует изменение значений переменных и особую роль оператора присваивания в системе Maple. В частности, в этом примере переменные х, у и z взаимосвязаны с помощью операций присваивания. Поэтому задание значения 2 переменной z приводит к тому, что и переменные у и х принимают то же значение.
Другой распространенный оператор — оператор равенства = используется для задания равенств и логических условий (например, а=b), указания областей изменения переменных (например, i=1..5 означает формирование диапазона изменения i от 1 до 5) и определения значений параметров в функциях и командах (например, color=black для задания черного цвета у линий графиков).
Операторы сами по себе результат не возвращают. Но они, наряду с функциями и своими параметрами (операндами), позволяют конструировать математические выражения, которые при их вычислении также возвращают результат.
С позиции канонов символьной математики квадратный корень из двух уже является основным результатом вычислений. Поэтому такая функция обычно не вычисляется в численном виде, а выводится в естественном виде, с применением знака квадратного корня √. Для вычисления в привычном виде (в виде десятичного числа с мантиссой и порядком) надо воспользоваться функцией evalf(sqrt(2)) — эта функция обеспечивает вычисление символьного выражения, заданного ее параметром (числом 2). Результат точных целочисленных операций Maple стремится представить в виде рационального числа — отношения двух целых чисел. Например:
> (125-2)/(3980+58);
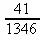
1.11.3. Операторы и средства вывода выражений
Для вывода выражений чаше всего используется оператор-символ «точка с запятой», который ставится после соответствующего выражения. Однако есть и оператор вывода print:
> print(2*sin(1));
> print(2*sin(1.));
Обратите внимание на несколько необычный вывод в этом примере (до сих пор вывод каждого выражения шел после его завершения). Такой вывод обеспечивается, если строки ввода ряда выражений заключены в общую квадратную скобку слева от приведенных выражений. Для блокирования вывода используется оператор «двоеточия», а оператор «%» применяется для исполнения предшествующего выражения:
> print(2*sin(1.)):
> 2*sin(1.):
> %;
Обратите внимание и на то, что знак «двоеточия» в первом случае не сработал. Это связано с тем, что сам оператор print выполнил свою функцию — вывода.
Некоторые выражения могут записываться в виде инертных функций, которые выводят записываемое выражение, но без их исполнения. Такие функции обычно записываются с большой буквы. Следующие примеры иллюстрирует применение функции интегрирования — обычной int и инертной Int:
> int(х^2,х=0..1);
> Int(х^2,х=0..1);
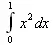
> evalf(%);
В первом примере Maple вычисляет интеграл предельно точно и дает ответ в виде рационального числа. Во втором примере просто выводится запись интеграла в математической нотации. В третьем случае функция evalf вычисляет этот интеграл и возвращает результат уже в форме числа с плавающей точкой. Мы еще вернемся в дальнейшем к более подробному описанию этих и иных средств вывода.
1.11.4. Обработка и индикация ошибок
При работе с системой Maple надо строго придерживаться правил корректного ввода выражений и иных объектов Maple-языка, называемых синтаксисом языка.
Алгоритмические, но синтаксически корректные, ошибки часто могут не распознаваться системой. Например, если в выражении a*sin(x) вы вместо аргумента х взяли аргумент b, то есть записали a*sin(b), то такую ошибку Maple распознать не может, ибо синтаксически как a*sin(x), так и a*sin(b) абсолютно корректны. Если вы перепутаете синус с косинусом и запишете a*cos(x), то такая ошибка также не будет распознана.
Ошибки в записи выражений, описывающих те или иные алгоритмы вычислений, не нарушающие синтаксическую корректность, системой Maple не распознаются. Контроль за такими ошибками целиком лежит на пользователе. Приведем еще один характерный пример ошибки, которую Maple не может распознать. Вводя выражение X/Y*Z, мы можем предположить, что это означает X/(Y*Z). Однако в Maple приоритет операций деления и умножения одинаков. Поэтому Maple вначале делит X на Y, а затем полученный результат умножает на Z:
> X/Y*Z:
> %;
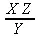
Ошибки такого рода называют семантическими. Если бы мы не проверили вывод с помощью оператора вычисления предыдущего выражения (%), то эта ошибка осталась бы нераспознанной. Выявление и устранение семантических ошибок выполняется на этапе отладки вычислений и программ.
Используйте блокировку вычислений с помощью знака двоеточия только в том случае, когда вы абсолютно уверены в правильности записи выражения — например, когда она очевидна и без повторения в строке вывода. Иначе вы можете не заметить вкравшейся в вычисления серьезной ошибки. В нашем примере мы получили бы верный результат, заключив выражение Y*X в круглые скобки. Как обычно, они предназначены для задания явного приоритета выполнения операций — в нашем случае вначале будет вычислено выражение в скобках (Y*Z), а затем уже X будет поделено на это выражение:
> X/(Y*Z);
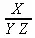
Но вернемся к ситуации с синтаксическими ошибками , которые система Maple распознает с помощью встроенного в нее синтаксического анализатора. Например, если вы задали неправильное имя функции, то это будет опознано синтаксическим анализатором и вычисления не будут выполняться. Maple просто повторит выражение в строке вывода:
> son(1.0);
В этом примере вместо имени функции sin введено ошибочное имя son. Maple воспринимает его как некую, введенную пользователем, функциональную зависимость, и потому просто повторяет запись и не выводит сообщение об ошибке. А вот другая ситуация — имя функции sin введено верно, но вместо десятичной точки при задании вещественного числа 1.0 использована запятая:
> sin(1,0);
Error, (in sin) expecting 1 argument, got 2
В данном случае Maple «знает», что работа идет с его встроенной функцией синуса, которая должна иметь единственный аргумент. Задание (1,0) означает, что пользователь ввел вместо вещественного числа два целочисленных числа, разделенных запятой. На это Maple отреагировал выдачей сообщения об ошибке (на экране дисплея оно имеет малиновый цвет). Исправьте ошибку, и синус единицы будет благополучно вычислен:
Читать дальшеИнтервал:
Закладка:










