Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

> sin(1.0);

А вот еще одна типичная ситуация — в последовательности выражений опущен знак-разделитель (двоеточие или точка с запятой):

> X:=2: Y:=3| Z:=4:

Error, missing operator or ';'

Тут Maple не только реагирует на ошибку, но и пытается подсказать, что именно пропущено. Более того, маркер ввода в виде мигающей вертикальной черточки будет помешен на место ошибки, и вы сможете тут же устранить ошибку. Правда, подсказки не всегда точны — в нашем случае явно пропущен разделитель в виде двоеточия, a Maple сообщает о пропуске точки с запятой. Впрочем, откуда системе знать, хотим мы вывести результат операции Y:=4 сразу (для этого нужен разделитель в виде точки с запятой) или откладываем на потом (с помощью символа двоеточия).

Вот еще один пример характерной ошибки — три знака * подряд:

> 2**|*3*sin(1.);

Error, `*` unexpected

Здесь Maple подсказывает, что один оператор * надо убрать — два знака * подряд означают вполне законный вариант оператора — возведение в степень. При этом маркер ввода вновь указывает место ошибки. Проанализируйте следующие простые примеры:

> 2**3*sin(1.);

> 2^3*sin(1.0);

> 2^(3*sin(1.0));

В двух первых примерах Maple вначале вычисляет функцию синуса, затем производит возведение в степень и лишь потом операцию умножения. Впрочем, такой приоритет операций принят практически во всех системах компьютерной математики и в языках программирования. Третий пример показывает изменение приоритета с помощью круглых скобок.

Достаточно опытному пользователю системой Maple большим подспорьем в эффективной работе с системой является контекстно-зависимое меню правой клавиши мыши. Для его применения достаточно навести курсор мыши на нужный объект (например, ячейку ввода или вывода, график и т.д.) и нажать правую клавишу мыши. Появится контекстное меню, в котором и можно выбрать ту или иную позицию или команду.

Удобство контекстного меню заключается в том, что оно всегда содержит только те команды, которые относятся к выбранному объекту. Контекстных меню в Maple великое множество и на копиях экрана примеров время от время будут приводиться разные варианты этого меню. Например, на рис. 1.19 показано контекстное меню двумерного графика с открытой позицией Style, позволяющей выбрать различный стиль линий графика. Позиция контекстного меню Export As открывает список графических форматов файлов, в которых может быть сохранен рисунок, представленный в графическом окне.

Если установить указатель мыши на входной ячейке, то это меню будет содержать три важные команды:

Standard Math — включает и выключает показ входных выражений в естественной математической форме;

Maple Input — управляет видом ячейки ввода (математический/текстовый);

Execute — включает выполнение ячейки.

Также, в зависимости от состояния буфера обмена и наличия выделения, в контекстном меню могут присутствовать команды Cut, Сору и Paste.

Левая кнопка мыши может использоваться для передачи фокуса или переноса маркера ввода, а также выделения частей документа.

На рис. 1.20 показан ряд простых вычислений. Среди них задание функции пользователя f(x) с одним параметром х. Нетрудно заметить, что параметр указывается в скобках после имени функции, а для записи выражения функции используется знак присваивания := (двоеточие со знаком равенства). Это старый способ задания функции пользователя, который (что видно из приведенного примера) еще работает, но уже не рекомендуется к применению.

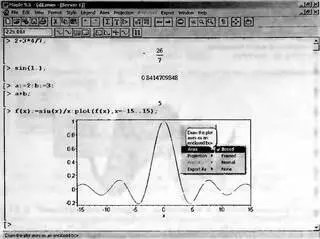
Рис. 1.20. Примеры простых вычислений с построением графика функции пользователя одной переменной

Для построения графика функции f(x) одной переменной используется функция plot в форме

plot(f(x), X = -15..15);

Нетрудно заметить, что при наличии нескольких параметров функции (в нашем случае их два) они разделяются запятыми. Выражение х=-15..15 задает, во-первых, указание, относительно какой переменной строится график, а во-вторых, говорит, в какой области значений меняются значения этой переменной — в нашем случае от -15 до +15. Шаг изменения переменной выбирается автоматически, в зависимости от размеров и вида графика.

Столь же просто, как и график обычной функции в декартовой системе координат, можно построить график трехмерной поверхности. Это показано на примере рис. 1.21. В данном случае задана функция двух переменных z(x,y) в рекомендуемом виде — z:=(x,y)->sin(x*y) и ее график строится с использованием графической функции plot3d. Правила задания пределов изменения переменных х и у соответствуют описанным выше. В данном случае можно было бы задать функцию пользователя и по старинке в виде z(x,y):=sin(x*y).

При выделении графика щелчком левой клавиши мыши на нем график обрамляется рамкой с местами ввода, за которые можно цепляться курсором мыши и растягивать график в ту или иную сторону. Кроме того, мышью при нажатой левой клавише можно вращать график в ту или иную сторону. Ряд возможностей форматирования графика дает контекстное меню правой клавиши мыши, показанное на рис. 1.21. С ними нетрудно разобраться самостоятельно.

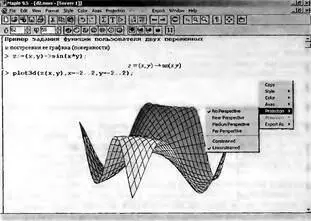
Рис. 1.21. Построение графика трехмерной поверхности, заданной функцией пользователя

Возможно, многих читателей вполне удовлетворят уже описанные возможности, но сила системы Maple 9.5 прежде всего в возможности выполнения аналитических (символьных) вычислений. Поэтому мы перейдем обсуждению некоторых из них.

Maple 9.5, как и другие СКА, открывает обширные возможности выполнения символьных ( аналитических ) вычислений. Мы уже описывали примеры решения квадратного уравнения. Возьмем еще один простой пример — требуется найти сопротивление трех параллельно включенных резисторов R1, R2 и R3 произвольной величины. Из курса электротехники известно, что можно задать следующее равенство, определяющее суммарное сопротивление R0.

> eq:=1/R0=1/R1+1/R2+1/R3;

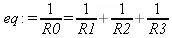
Теперь достаточно использовать функцию решения уравнений solve, чтобы найти значение R0 в общей аналитической форме: