Владимир Дьяконов - Maple 9.5/10 в математике, физике и образовании

К примеру, попытка вычислить в общем виде выражение sin(x)²+cos(x)²=1 с помощью численных математических систем или программ на обычных языках программирования к успеху не приведет. Вместо ожидаемого результата появится сообщение об ошибке вида: «Переменная х не определена!».

СКА не только не боятся применения неопределенных переменных , но и предпочитают работать с ними. Зададим, к примеру, в Maple 9.5 квадратное уравнение, присвоив его выражение переменной eq (файл solve):

> eq:=a*x^2+b*x+c=0;

Проверим статус переменной х .

> х;

Переменная просто повторена в выводе, что и указывает на то, что она неопределенная. Теперь попробуем решить уравнение, используя функцию solve:

> solve(eq,x);

Получено хорошо известное решение для квадратного уравнения. А теперь попробуем найти аналитическое решение для других переменных a, b и с:

> solve(eq,а);

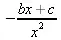
> solve(eq,b);

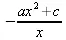
> solve(eq,с);

Решение прошло успешно — во всех случаях пoлvчeны аналитические выражения для решения. Они более тривиальные, чем решение eq относительно х.

Не следует считать решения в аналитическом виде ограничением СКА. Большинство СКА, в том числе и Maple 9.5/10 легко решают подавляющее большинство задач и в численном виде и являются универсальными СКМ. Так, определив переменные а, b и с, присвоением им некоторых значений

> а:=2:b:=3:с:=4:

получим решение в численном виде:

> solve(eq,х);

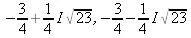
Оно получено в виде комплексно-сопряженных чисел, в них I это мнимая единица, т. е. √-1.

В последних реализациях Maple много внимания было уделено повышению скорости вычислений. Система Maple 8, к примеру, вычисляла факториал максимально возможного числа 32000, затрачивая на это (на ПК с процессором Pentium III 600 МГц) 2,784 с [22]. A Maple 9.5 на современном ПК с процессором Pentium 4 Hyper Threading 2,6 ГГц справляется с этим в более чем в двадцать раз быстрее (файл bench):

> restart: t := time(): 32000!: TIME-time()-t;

Разумеется, выигрыш в скорости в данном случае обусловлен как применением более скоростного компьютера, так и системы Maple 9.5. К примеру, на том же компьютере Maple 8 выдала результат за 0,583 с, a Maple 7 — 0,610 с. Таким образом, скорость вычисления у Maple 9.5 в данном случае (при равных аппаратных возможностях) оказалась выше более чем вдвое. Любопытно, что при повторном выполнении этой команды время выполнения было показано нулевым, что свидетельствует об эффективном кэшировании программных кодов.

Обратите внимание на примененный полезный прием оценки скорости вычислений с помощью функции time() без аргумента. Можно подыскать и куда более эффектные частные примеры. Например, сумма 100000 членов 1/k^2 в Maple 8 вычислялась на ПК автора с процессором Pentium 4 НТ 2,6 ГГц за время около 256 с:

> t := time():add(1/k^2, k=1..100000): TIME=time()-t;

А в Maple 9.5 тот же пример дал время меньше 7 с:

> t := time() :add(1/k^2, k=1..100000): TIME=time()-t;

В данном случае резкое ускорение вычислений обусловлено применением новой библиотеки целочисленной арифметики — GNU Multiple Precision (GMP).

Доброго обывателя в области математики поражает способность Maple выполнять точные арифметические операции с целыми числами, которые не помешаются в строку. При этом знак \ переносит вывод на следующую строку, а знак % подставляет в строку ввода результат предшествующей операции:

> 200!+123456789;

> %-200!;

Но Maple 9.5 идет еще дальше — почти мгновенно (особенно при повторе примера) система вычисляет факториал 100000:

> t : = time():bigFactorial := 100000!:TIME=time()-t;

> t := time():bigFactorial := 100000!:TIME=time()-t;

Заметно повышена и скорость многих сложных вычислений. Например, на вычисление внушительного определенного интеграла

> Int( х^n*ехр(-х^n) + Sum( cos(k*x)/k, k=1..n), х=0..1);

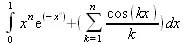
в стократно повторяющемся цикле, Maple 9.5 затрачивает чуть меньше трех сотых секунды на каждое вычисление интеграла:

> t := time():

for i from 1 to 100 do

evalf(Int(х^i*ехр(-x^i) + add(cos(k*x)/k, k=0..i), x=0..1)):

end do:

TIME=time()-t;

В следующем примере вычисляется время, которое нужно для создания большой матрицы случайных чисел с помощью пакета расширения LinearAlgebra:

> М := LinearAlgebra:-RandomMatrix(500);

> timeconsumed = time(type(M, 'Matrix'(algebraic)));

Повышение скорости вычислений обеспечено усовершенствованием алгоритмов численных вычислений (например, GNU) и применением подпрограмм национальной группы алгоритмов NAG — общепризнанных в области быстрых вычислений при решении задач линейной алгебры. Кстати, выше была приведена первая программа на Maple-языке программирования, использующая конструкцию цикла.

Читатели книги [23], описывающей предшествующую реализацию Maple 9, обратят внимание на то, что данные по скорости выполнения операций у Maple 9.5 лишь немного отличаются от приведенных для Maple 9, причем в ту или иную сторону. Это позволяет считать их практически равноценными.

Любопытно отметить, что последний пример в Maple 10 дал при первом пуске время 0.078 с, а при втором 0.015. Это говорит о том, что слишком щепетильно относиться к подобным тестам не стоит. Они дают лишь порядок величин, характеризующих скорость вычислений.

Как у всех приложений под Windows интерфейс Maple 9.5 имеет ряд характерных элементов, отчетливо видимых на рис. 1.2, 1.3 и 1.4:

• строка заголовка (сверху);

• строка главного меню;

• главная панель инструментов;

• контекстная панель инструментов, вид которой зависит от режима работы с Maple 9.5;

• окно ввода и редактирования документов;

• строка состояния (в самом низу окна);

• панели ввода специальных математических символов (см. ниже).

Пользовательский интерфейс Maple 9.5 позволяет готовить документы, содержащие одновременно текстовые комментарии, команды входного языка (с возможным преобразованием их в естественную математическую форму нажатием кнопки с буквой «х»), результаты вычислений в виде обычных математических формул и графические данные. Это обеспечивает понятное представление исходных данных и результатов вычислений, а также удобство их повторного использования.