Генри Дьюдени - Пятьсот двадцать головоломок

Другой вариант. Предположим, что партия развивалась следующим образом: 3—1, 1—2, 3—3, 1—2, 1—4, счет стал 21, и второй игрок снова должен выиграть, поскольку не осталось ни одной карты с 1 очком и первый игрок на следующем ходу вынужден превзойти сумму 22 очка.

Кто из игроков может всегда выиграть и как он должен при этом действовать?

463. Игра в девять квадратов.Начертите простую диаграмму, изображенную на рисунке, и возьмите коробок спичек. Длина стороны большого квадрата равна трем спичкам. Игра состоит в том, чтобы, выкладывая поочередно по одной спичке, окружить большее число малых квадратиков, чем окружит ваш противник. Замкнув маленький квадратик, вы не только получаете одно очко, но и ходите снова вне очереди [26] Если у вас есть возможность замкнуть какой-нибудь квадратик, но вы считаете это нецелесообразным, вы имеете право этого не делать, однако, замкнув квадратик, вы обязаны ходить. — Прим. перев. . Здесь изображена одна из партий. Я и мой противник выложили по шесть спичек, а поскольку начинал я, то теперь моя очередь ходить.

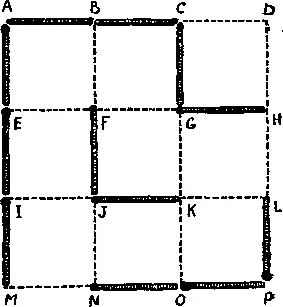
Какой ход будет для меня наилучшим? Если я пойду на FG , то мой противник пойдет на BF и выиграет очко. Далее, поскольку он получает право внеочередного хода, то он пойдет на EF , а затем на IJ и на GK . Если теперь он пойдет на CD , то мне не останется ничего лучшего, как пойти на DH (получив при этом одно очко); но, поскольку я должен буду снова ходить вне очереди, все остальные квадратики достанутся моему противнику. В результате я проиграю с «разгромным» счетом 8 : 1.

Как я должен пойти вместо «рокового» хода на FG ? Во многих партиях игры в 9 квадратов есть над чем подумать. Ни одна из партий не может закончиться вничью.

464. Десять карт.Разложите десять игральных карт, как показано на рисунке. Играют двое. Первый игрок может перевернуть любую карту. Затем второй игрок может перевернуть две соседние карты или одну карту и т. д. Выигрывает тот из игроков, который перевернет последнюю карту.

Помните, что вначале первый игрок должен перевернуть одну карту, а затем каждый из игроков перевертывает либо одну, либо две соседние карты.

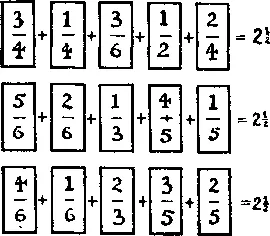
465. Дроби из домино.Возьмите обычный набор домино и удалите из него все дубли и пустышки. Затем рассматривайте оставшиеся 15 костяшек как дроби. На рисунке костяшки расположены таким образом, что сумма всех дробей в каждом ряду равна 2½. Однако все мои дроби правильные. Вам же разрешается использовать столько неправильных дробей (вроде , , , сколько вы пожелаете, лишь бы сумма в каждом ряду равнялась 10.

466. Головоломка с домино.Вы видите, что изображенные здесь две костяшки домино расположены таким образом, что, объединяя между собой группы очков, непосредственно прилегающие друг к другу, я могу получить все числа от 1 до 9 включительно. Так, 1, 2 и 3 можно взять «в готовом виде», 1 и 3 в сумме дают 4; 3 и 2 дают 5; 3 и 3 дают 6; 1, 3 и 3 дают 7; 3, 3 и 2 дают 8; а 1, 3, 3 и 2 дают 9. Не разрешается составлять 3 из 1 и 2 или 5 из первой 3 и 2, поскольку эти числа не прилегают друг к другу непосредственно.

Попытайтесь теперь расположить 4 костяшки домино так, чтобы аналогичным образом получить любое число от 1 до 23 включительно. Костяшки не обязаны располагаться 1 к 1, 2 к 2 и т. д., как во время игры.

467. Квадрат из домино.Выберите любые 18 костяшек домино из обычного комплекта и расположите их в виде квадрата, как вам заблагорассудится, лишь бы никакое число не повторялось дважды ни в одной из строк, ни в одном из столбцов. Пример, приведенный на рисунке, неудачен, так как, хотя ни одно число не повторяется дважды ни в одном из столбцов, три строки нарушают это условие. В первой строке расположены две четверки и две пустышки, в третьей строке — две пятерки и две шестерки, а в четвертой строке — две тройки.

Не могли бы вы составить квадрат, полностью удовлетворяющий нашим условиям? Пустышка рассматривается как число.

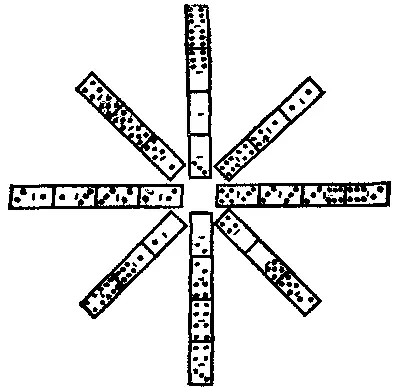
468. Звезда из домино.Расположите 28 костяшек так, как показано на рисунке, чтобы они образовали звезду с лучами из трех и четырех костяшек поочередно. Каждый луч должен содержать 21 очко (в нашем примере только один луч содержит столько очков), а в центре должны быть расположены числа 1, 2, 3, 4, 5, 6 и две пустышки (как в нашем примере) в любом порядке. В каждом луче костяшки должны прикладываться друг к другу по обычному правилу: 6 к 6, пустышка к пустышке и т. д.

469. Группы костяшек.Известно ли кому-нибудь из моих читателей, что если выложить все 28 костяшек домино в одну линию согласно обычному правилу (6 к 6, 2 к 2, пустышка к пустышке и т. д.), то числа на концах всегда совпадут между собой, так что на самом деле костяшки можно расположить по кругу? Очень старый трюк заключается в том, что, спрятав одну из костяшек (но не берите дубль), вы просите кого-нибудь расположить остальные костяшки в линию, а сами отворачиваетесь. Зрителей поражает, когда вы, не глядя на то, что получилось, называете числа, стоящие на концах. Эти числа совпадают с теми, что стоят на вашей убранной костяшке, поскольку все костяшки образуют круг. Если мы расположим костяшки так, как показано на рисунке, а затем разорвем цепочку на четыре куска, по 7 костяшек в каждом, то можно обнаружить, что сумма очков в первой группе равна 49, во второй 34, в третьей 46 и в четвертой 39.

Мне хотелось бы составить из костяшек 4 группы так, чтобы суммы очков в каждой из групп были равны между собой. Можете ли вы это сделать?

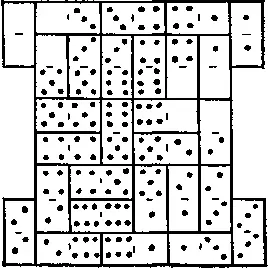
470. Кадрили.Вот одна старая французская головоломка, которая, как мне кажется, заинтересует читателей. Требуется расположить полный комплект из 28 костяшек домино в виде фигуры, изображенной на рисунке, причем все числа должны образовать серию квадратов. Так, в верхних двух строках мы видим квадрат из пустышек, квадрат из троек, квадрат из четверок и квадрат из единиц; в третьей и четвертой строках стоят квадраты из пятерок, шестерок и пустышек и т. д. Это и в самом деле решение данной головоломки, как ее обычно формулируют. Однако я прошу найти такое расположение, которое не содержало бы пустышек на внешней границе. В нашем примере на границе можно найти все числа от пустышки до шестерки включительно.