Генри Дьюдени - Пятьсот двадцать головоломок
- Название:Пятьсот двадцать головоломок
- Автор:
- Жанр:
- Издательство:Мир
- Год:1975
- Город:Москва
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Генри Дьюдени - Пятьсот двадцать головоломок краткое содержание
Генри Э. Дьюдени по праву считается классиком занимательной математики. Многие его задачи, породив обширную литературу и вызвав многочисленные подражания, вошли в ее золотой фонд.
В предлагаемой книге собрано 520 задач и головоломок Дьюдени по арифметике, алгебре, геометрии, разрезанию и составлению фигур. Читателя ждет встреча с постоянно действующими героями Дьюдени — семейством Крэкхэмов, профессором Рэкбрейном и др.
Книга доставит удовольствие всем любителям занимательной математики.
Пятьсот двадцать головоломок - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
366. Меняйте пары местами следующим образом: (1—7, 7—20, 20—16, 16—11, 11—2, 2—24), (3—10, 10—23, 23—14, 14—18, 18—5), (14—19, 19—9, 9—22), (6—12, 12—15, 15—13, 13—25), (17—21) . Теперь все фишки правильно размещены за 19 ходов. Внутри скобок заключены полные циклы. Выпишите числа в исходном порядке, а под ними числа в правильном порядке так:
| 7 | 24 | 10 | 19 | 3 | 12 | 20 | 8 | 22 | и т. д. |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | и т. д. |
Структура циклов становится теперь очевидной: 1 в нижней строке меняется местами с 7 над ней, 7 — с 20 и т. д. до тех пор, пока мы не дойдем до 24 под 1.
367. Пусть солдаты двигаются в следующем порядке: 2 —1, 3 —2, 4 —3, 5 —11, 6 —4, 7 —5, 8 —6, 9 —7, 1 —13, 9 —10, 8 —9, 1 —12, 7 —13, 6 —8, 5 —7, 1 —11, 4 —12, 3 —6, 2 —5, 1 —1, 2 —2, 3 —3, 4 —4, 5 —5, 6 —6, 7 —7, 8 —8, 9 —9 ; тогда сержант окажется на нужном месте за 28 ходов.
Первое число — это номер солдата, а второе — номер его новой позиции, причем позиции в траншее перенумерованы от 1 до 10, а ниши от 11 до 13.
368. В первом случае передвигайте пары в следующем порядке: поместите 6 и 7 перед 1 , затем 3 и 4 , 7 и 1 и 4 и 8 на свободные места. При этом получится следующее расположение фишек: 6, 4, 8, 2, 7, 1, 5, 3 .
Во втором случае передвиньте фишки 3, 4 и расположите их в обратном порядке ( 4, 3 ) перед фишкой 1 . Затем переместите, одновременно изменив порядок фишек на обратный, пары 6, 7 (после перестановки 7, 6 ), 6, 5 (после перестановки 5, 6 ), 3, 1 (после перестановки 1, 3 ) и 6, 8 (после перестановки 8, 6 ). Фишки выстроятся в последовательности 4, 8, 6, 2, 7, 1, 3, 5 всего за 5 ходов.
369. Хотя первоначально обе буквы A находятся в нужном положении, головоломку можно решить, только сдвинув их со своего места. Обозначим букву A в нижнем ряду прописной, а в верхнем углу строчной буквой. Тогда решение в 36 ходов будет таким: АНЛЕЖ АНЖКИ АНЖКИ АНЖКЛ ЕаАНЖ ИЛКИЛ аЕКаЛИ.
[Решение Дьюдени не минимально. Не сможет ли читатель решить головоломку за 30 ходов? — М. Г. ]
370. Передвигайте фишки в следующем порядке: АНДАФ ЛНДАФ ДНЛДИ ЯДЛНА ФИЯРИ ЯЛНАЛ — всего 30 ходов.
[Количество ходов удается сократить до наименьшего возможного числа — 28. Читатели могут заметить, что задача изоморфна некоторой головоломке с квадратом и восьмью фишками, похожей на предыдущую. С общей теорией головоломок с квадратом и фишками можно познакомиться в гл. 2 книги М. Гарднера «Математические головоломки и развлечения» (М., изд-во «Мир», 1971). — М. Г. ]
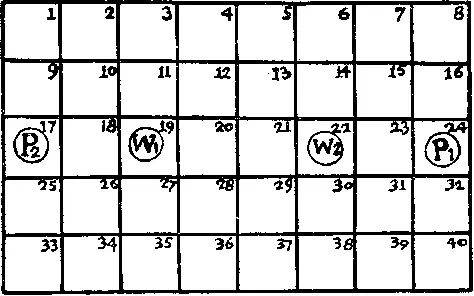
371. Охранник W 1, не может схватить узника P 2, а охранник W 2 — узника P 1. В примере, который мы привели, погоня действительно может продолжаться бесконечно долго, поскольку на самом деле каждый охранник должен охотиться не за «своим», а за «чужим» узником. В этом случае, как говорят о шахматах, можно «реализовать преимущество». Между W 1и P 2расположен всего один (нечетное число) квадрат, в то время как между W 1и P 1(а также между W 2и P 2) имеются четыре (четное число) квадрата. Во втором случае у охранников имеется преимущество, и они могут выиграть. Приведем образец игры. Ходы охранников записываются в «числителе», а узников — в «знаменателе»:
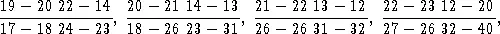
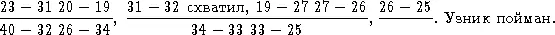
Узникам невозможно уйти от преследования, если каждый охранник преследует того из них, кого нужно.
372. В средней вертикали, содержащей 3 белые и 3 черные шашки, их можно поменять местами за 15 ходов. Перенумеруйте 7 клеток сверху вниз цифрами от 1 до 7. Шашкой, стоящей на клетке 3 , пойдите на клетку 4 , шашкой 5 — на клетку 3 , 6 — на 5 , 4 — на 6 , 2 — на 4 , 1 — на 2 , 3 — на 1 , 5 — на 3 , 7 — на 5 , 6 — на 7 , 4 — на 6 , 2 — на 4 , 3 — на 2 , 5 — на 3 , 4 — на 5 . Шесть из этих ходов представляют собой просто сдвиги, а 9 остальных — прыжки.
Имеется семь горизонталей, содержащих по 3 белые и по 3 черные шашки (если исключить центральную вертикаль). В каждой из них можно аналогичным образом поменять местами белые и черные шашки, а поскольку в процессе манипуляций с центральной вертикалью в центре каждой из горизонталей образуется в определенный момент необходимое для этого «окошко», то ясно, что все шашки можно поменять местами за 8 × 15 = 120 ходов.
373. Сначала положите 4 монеты вместе, как показано в случае 1 , затем перенесите номер 1 на новое место (см. случай 2 ) и, наконец, осторожно выньте номер 4 и положите его сверху на номера 2 и 3 . Тогда ваши монеты займут положение 3 и пятую монету можно будет точно подогнать к ним.
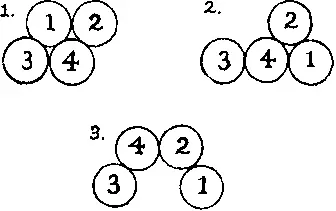
Одного взгляда на рисунок достаточно, чтобы понять, как трудно измерить на глаз расстояние между монетами 1 и 3 . Почти наверняка каждый положит их слишком близко друг к другу.
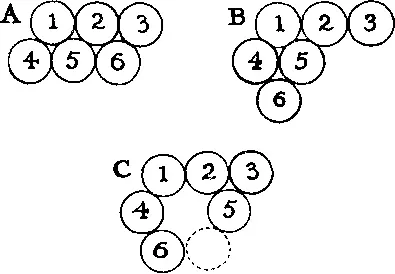
374. Сначала разместите монеты так, как показано в случае A . Затем осторожно сместите монету 6 в положение, которое изображено в случае B . Далее сделайте так, чтобы монета 5 соприкоснулась с монетами 2 и 3 ( C ). Теперь нужно переместить монету 3 в положение, указанное в случае C пунктиром.
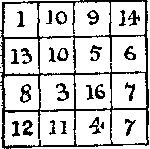
375. Взяв вместо чисел 2 и 15 числа 7 и 10, можно составить квадрат, показанный на рисунке. Практически магический квадрат пы составите из любых 16 чисел, если их удастся расположить таким образом, чтобы были равны между собой как все разности между двумя соседними числами по горизонтали, так и все разности между двумя соседними числами по вертикали. В нашем случае эти разности равны 3 и 2:
| 1 | 4 | 7 | 10 |
| 3 | 6 | 9 | 12 |
| 5 | 8 | 11 | 14 |
| 7 | 10 | 13 | 16 |
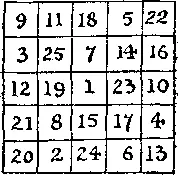
376. Если вы сделаете 9 квадратов, совпадающих с квадратом, изображенным на нашем рисунке, то, составив из них больший квадрат, обнаружите на нем магические квадраты пятого порядка с любым числом в центре. Этот квадрат называется назикским квадратом (названным так покойным мистером Фростом в честь Назика — места в Индии, где он жил) и является единственным правильным квадратом с таким свойством.
Читать дальшеИнтервал:
Закладка:






![О Генри - Через двадцать лет [After Twenty Years]](/books/1083375/o-genri-cherez-dvadcat-let-after-twenty-years.webp)

